Conteúdo deste artigo
Introdução
Não é recente o fascínio do homem pelos números. Caso estivéssemos procurando diferenças entre o interesse do passado e do presente do homem em relação aos números, encontraríamos como a principal, o fato de que antes o estudo numérico era feito apenas pela busca pelo conhecimento, por prazer. Ao contrário de hoje em dia, onde eles são estudados como forma de desenvolvimento tecnológico e científico, bem como para manutenção do sistema capitalista vigente.
Pesquisas históricas mostram que pensadores gregos, por volta de 2500 anos atrás, foram os pioneiros no estudo prazeroso dos números. Esse estudo gerou muitas descobertas sobre os números naturais, como, por exemplo, a relação entre números e formas geométricas.
Números e figuras geométricas
Os gregos perceberam que se podia formar figuras geométricas, planas e espaciais, a partir de números naturais. Um exemplo disso são os números 3, 6, 10... que podem formar triângulos. Veja:
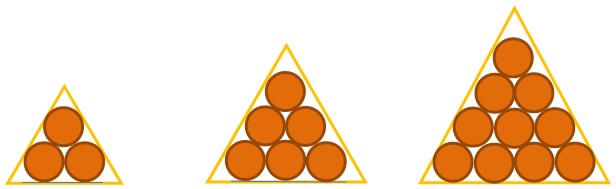
Perceba que não conseguiremos formar triângulos com os números 2, 4, 5, 7...
Os números naturais que podem ser arrumados de maneira a formar triângulos são chamados de números triangulares.
Seguindo essa mesma linha de raciocínio, encontraremos números que, quando devidamente arrumados, são capazes de formar cubos. Acompanhe:

1

2

3
No exemplo anterior, os números 1, 8 e 27 são números cúbicos, por formarem cubos de acordo com sua devida distribuição.
Foi montando figuras geométricas e associando números naturais a elas que os gregos perceberam que havia números com maior grau de importância do que outros. Por aparecer na formação de todo e qualquer número, seria o 1 o número mais importante de todos? Por exemplo: 2 = 1 + 1, 3 = 1 + 1 + 1 ... Constatou-se que, se estamos tratando apenas da adição, sim, o número 1 é o mais importante de todos. Porém, quando migramos para o campo da multiplicação, o 1 não forma nenhum novo número, perdendo a sua importância (1 é elemento neutro da multiplicação).
Se tomarmos como ponto de partida, na multiplicação, o número 2, veremos que ele é capaz de gerar uma infinidade de outros números: 2 . 2 = 4; 2 . 2 . 2 = 8; 2 . 2 . 2 . 2 = 16... Porém, ao mesmo tempo, perceberemos que a multiplicação de nenhum outro número natural por ele mesmo será capaz de gerar o número 2. Com isso concluímos que o 2 é gerador de outros números naturais, mas não pode ser gerado pela multiplicação de nenhum deles. Nesse ponto, está claro que o 2 é capaz de gerar infinitos números, mas não é capaz de gerar todos os números possíveis. Por exemplo, apenas por multiplicação de fatores 2 não chegaremos ao número 6, nem ao 7, nem ao 9 etc. Com isso, os gregos concluíram que existem outros números geradores, que não apenas o 2.
Peguemos o número 60 e analisemos a sua formação: 30 = 2 . 3 . 5, ou seja, o número 60 é formado pelos fatores 2, 3 e 5. Os números naturais formadores de outros números naturais por meio da multiplicação foram chamados números primos.
Os números primos ganharam elevado grau de importância na concepção grega. Eles são os geradores de todos os números naturais, mas nenhum número natural é capaz de gerá-los. Para concluir, aqueles números que são gerados a partir da multiplicação de números primos são chamados números compostos.
Considerações finais
Diante de todo o exposto neste trabalho, ainda sobra as seguintes indagações: e o 0 e o 1, são primos ou compostos? A resposta é simples, nem primos, nem compostos. Na verdade, nem o 0 e nem o 1 se encaixam nas definições de números primos e compostos.
Essa contribuição dos gregos para o avanço da matemática ilustra a importância desse povo para o desenvolvimento de toda a humanidade. Os seus pensamentos e descobertas podem ser encontrados nos mais diversos campos do conhecimento humano: educação, matemática, arquitetura, engenharia etc. Os gregos viveram numa época em que o pensamento tinha valor, o maior dos prêmios era apenas a descoberta, pelo maravilhoso prazer de descobrir. Hoje, em pleno século XXI, com o uso desnorteado da internet e das várias tecnologias, percebemos o encurtamento de espaço sobre o pensamento humano, capaz de criar, descobrir, redescobrir e modificar o mundo.
Referência bibliográfica:
IMENES, Luiz Márcio. LELLIS, Marcelo. Matemática. – 2 ed. – São Paulo: Moderna, 2012.
Texto originalmente publicado em https://www.infoescola.com/matematica/numeros-geradores-de-outros-numeros/