Os números primos fascinam matemáticos há mais de 2000 anos. Os números primos são o santo graal da matemática pois, mesmo tendo uma definição tão simples muitos problemas que os envolvem ainda não estão solucionados. Vamos definir o que é um número primo:
Os números primos são aqueles em que possuem apenas dois divisores: 1 e o próprio número.
Agora, vamos identificar alguns números primos segundo a definição acima a partir do conjunto dos naturais N={0, 1, 2, 3, 4, 5, 6, ...} . Os números primos menores que 100 são:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
Os números 0, 1, 4, 6, 8, 10 e 12 não são primos pois possuem mais de um divisor, por exemplo, o 6 pode ser dividido por 1, 2, 3 e o próprio 6. O 8 é dividido por 1, 2, 4 e 8. O zero não pode ser primo, pois ele pode ser dividido por qualquer outro número que, ainda assim seria zero, o que nos leva uma infinidade de divisores. Já o 1 também não pode ser primo pois ele possui um único divisor, ele mesmo. O número 2 é o menor primo e o único par.
A complexidade começa aqui: Como saber se um número é primo ou não? Para números pequenos é fácil responder a esta pergunta, mas quando pensamos na infinidade de números naturais que existem, escolhermos um e ainda identificar se ele é primo ou não, é um desafio e tanto! Infelizmente, não existe uma fórmula que determine se um número é, ou não, primo, mas há diversas ferramentas para nos ajudar nesta tarefa. O método mais conhecido é o Crivo (ou Algoritmo da Divisão) de Eratóstenes.
Este método consiste basicamente em testar se o número é, ou não, divisível por algum número natural menor do que ele próprio. Vamos agora mostrar como o Crivo de Eratóstenes funciona para determinar todos os números primos de 1 a 100:
- Escreva todos os números de 1 a 100 numa tabela.
- Elimine todos os múltiplos de 2, exceto o próprio 2 que já sabemos que é primo.
- Depois, faça isto com os múltiplos de 3, exceto o 3 que também é primo.
- O próximo da lista não riscado seria o 5, risque os múltiplos também.
Seguindo este método recursivamente, como vemos na tabela abaixo, os números verdes são os primos, os outros são números que são múltiplos de algum primo:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Teorema de Eratóstenes
Dado 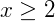 , para garantirmos que é primo basta mostrar que nenhum número primo
, para garantirmos que é primo basta mostrar que nenhum número primo 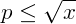 divida x.
divida x.
Isto significa que para determinarmos se um número 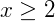 é primo, dividimos sucessivamente x até somente
é primo, dividimos sucessivamente x até somente 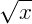 . Se uma dessas divisões for exata, constatamos que x não é primo. Do contrário, se nenhuma for exata, então x é primo. No caso acima, como
. Se uma dessas divisões for exata, constatamos que x não é primo. Do contrário, se nenhuma for exata, então x é primo. No caso acima, como 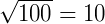 , então bastaríamos eliminar os múltiplos de 2, 3, 5 e 7.
, então bastaríamos eliminar os múltiplos de 2, 3, 5 e 7.
Teorema Fundamental da Aritmética (T.F.A.)
Todo número inteiro maior do que 1, 0 e -1 pode ser escrito (ou decomposto) pelo produto de fatores primos de forma única.
Exemplos:
- O número 15 pode ser escrito como (3.5), onde 3 e 5 são primos;
- 28 = 2.2.7 (2 e 7 são primos)
- 135 = 3.3.3.5
Se elevarmos qualquer número inteiro a uma potência de qualquer valor (2, 3, 4, ...) o T.F.A. continuará valendo, por exemplo:
- 152 = 32. 52 = 9 . 25 = 225
- 282 = 22.22.72 = 4.4.49 = 784
- 1353 = 33. 33. 33.53 = 27.27.27.125 = 2460375
Podemos então generalizar. Qualquer número inteiro x pode ser escrito da seguinte forma:
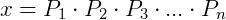
E se elevarmos esse número inteiro a qualquer potência de valor m teremos:
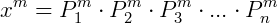
Sendo P1, P2, P3 ... Pn números primos.
A distribuição de primos é totalmente irregular e descobrir os seus segredos tem sido um objetivo para muitos matemáticos.
Referências Bibliográficas:
MILIES, César Polcino; COELHO, Sônia Pitta. Números: Uma Introdução à Matemática. São Paulo: EDUSP,2013.
HEFEZ, Abramo. Elementos da Aritmética. Rio de Janeiro: SBM, 2011.
Texto originalmente publicado em https://www.infoescola.com/matematica/numeros-primos/