Considere o número 0,010203040506...
Observando a formação desse número, vamos supor que podemos dar continuidade à sua parte decimal do seguinte modo:
0,01020304050607...;
0,0102030405060708...; e assim por diante.
Como a representação decimal desse número tem infinitas casas decimais e não é periódica, não podemos obter sua forma de fração, logo, esse número não é racional.
Agora, veja este outro número:
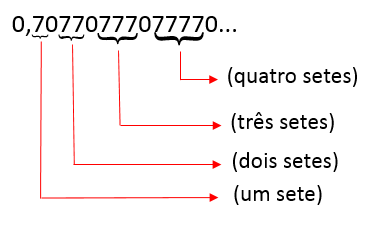
Imagine que, para continuar escrevendo esse número, devemos acrescentar sempre um algarismo 7 aos grupos de 7 separados por 0:
A representação desse número não é decimal exata nem periódica. Portanto, esse número não pode ser escrito na forma de fração. Logo, não é um número racional.
Com esses exemplos, percebemos que existem números que não são representados nem por uma forma decimal exata (com um número finito de casas decimais), nem por uma dízima periódica. Portanto, não podem ser escritos na forma de fração, isto é, na forma a/b com a e b inteiros e b≠0, logo, não são números racionais. Esse tipo de número é chamado de número irracional.
Agora, veja a representação decimal dos números 
e 
com sete casas decimais.
Por maior que seja o número de casas decimais usadas para representar esses números, nunca vamos encontrar para eles uma representação decimal exata ou periódica. Portanto, não há frações que os representem. Por isso, dizemos que e são números irracionais. Também é irracional toda raiz quadrada de um número natural que não seja quadrado perfeito, assim como toda raiz quadrada de fração positiva irredutível cujo numerador e denominador não seja quadrado perfeito.
Outros exemplos de números irracionais são: o número 
, que está relacionado com o cálculo do comprimento da circunferência; e do número e, que é uma constante matemática que é a base dos logaritmos naturais.
Para exemplificar alguns números irracionais, temos:
- A constante
(pi) possui infinitas casas decimais e não tem parte periódica; por isso, é um número irracional.
- é outro exemplo de número irracional.
Vários cálculos já foram feitos na tentativa de se chegar ao valor exato de 
, mas nunca se encontrou um decimal exato ou uma dízima periódica. Os matemáticos provaram que não é possível escrever esse número como quociente de dois inteiros e, por isso, não pode ser expresso como um decimal exato ou uma dízima periódica. Portanto, é um número irracional.
- O número ф (phi), também conhecido como número de ouro, tem infinitas casas decimais e não tem parte periódica. Esse número é irracional.
ф (phi) = 1,61803...
O número e, também chamado número de Euler, é outro exemplo de número irracional.
e = 2,7182818284590452353602874...
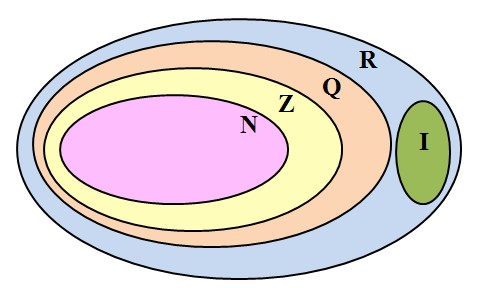
A união do conjunto dos números racionais (no qual estão contidos o conjunto dos números naturais e o conjunto dos números inteiros) com o conjunto dos números irracionais forma um novo conjunto chamado conjunto dos números reais, representado por 
.
Reta Real
É impossível representar, ponto a ponto, todos os números racionais, pois, entre dois números racionais, existe uma infinidade de outros números racionais. Mesmo que isso fosse possível, os pontos que representariam esses números não seriam suficientes para cobrir toda a reta numérica. Faltariam ainda os pontos correspondentes aos correspondentes números irracionais para completá-la.
A representação de todos os números reais, preenche a reta numérica. A essa reta chamamos de reta real.
Todo número real tem um único ponto correspondente na reta e qualquer ponto da reta tem um único número real correspondente.
Intuitivamente, dizemos que o conjunto dos números reais é formado por todos os números que podem ser representados na reta numérica. Para representar subconjuntos ou intervalos da reta real usamos a representação geométrica ou uma notação própria utilizada no estudo dos conjuntos.
Vejam o quadro abaixo que mostra alguns exemplos de como representar os intervalos dos números reais.
Texto originalmente publicado em https://www.infoescola.com/matematica/numeros-reais/