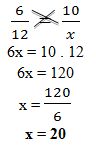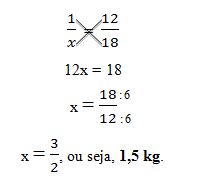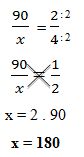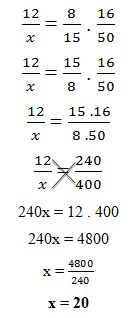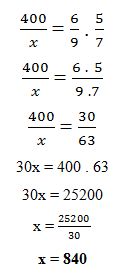Regra de Três Simples e Composta

Um pouco de história

Estuda-se em proporção a relação entre grandezas. Em alguns casos vemos que as grandezas são diretamente proporcionais, ou seja, o aumento de uma implica o aumento da outra, em outros, inversamente proporcionais, isto é, o aumento de uma implica a redução da outra. Seja em quaisquer dos casos anteriores, podemos resolver grande parte dos problemas relacionados às grandezas proporcionais utilizando regra de três simples ou composta.

O conhecimento e a utilização de conceitos semelhantes à regra de três são muito antigos, tendo sua provável origem na China antiga, podendo ser observados em tempos muito distantes. Vários problemas envolvendo manipulações muito próximas do que hoje conhecemos como regra de três podem ser vistos no Papiro Rhind, documento confeccionado no Egito há cerca de 3000 anos. Mais recente que o Papiro Rhind, o livro Liber Abaci do matemático italiano Leonardo Fibonacci (1175-1250) revela vários problemas envolvendo a regra de três.

Apesar de sua criação ser tão remota, as aplicações relativas à regra de três são as mais variadas. Tratando da matemática utilitária, podemos dizer que a regra de três é primordial a nossa vida, pois soluciona questões corriqueiras com muita simplicidade e economia de tempo.

Vejam abaixo alguns problemas envolvendo regra de três simples e composta, direta e inversamente proporcionais.

1. Um quilo (usarei “quilo” simplificadamente para representar quilograma (Kg)) de farinha de trigo é suficiente para fazer 12 pães. De quanta farinha necessito para fazer 18 pães?
2. Quatro pedreiros constrói uma pequena casa em 90 dias. Dois pedreiros construirá a mesma casa em quanto tempo?
3. Se 8 homens levam 12 dias montando 16 máquinas, então, nas mesmas condições, 15 homens levarão quantos dias para montar 50 máquinas?
4. Trabalhando 6 dias, 5 operários produzem 400 peças. Quantas peças desse mesmo tipo serão produzidas por 7 operários em 9 dias de trabalho?

Ainda neste artigo, em momento oportuno, solucionaremos os problemas propostos acima.

Grandezas diretamente proporcionais

Dizemos que duas grandezas são diretamente proporcionais quando o aumento de uma implica o aumento da outra. Ao dobrarmos uma grandeza, a outra também será dobrada, ao triplicarmos uma, a outra também será triplicada. Em outras palavras, grandezas diretamente proporcionais variam sempre na mesma razão.

Vejam o exemplo

Observação: A tabela acima é meramente ilustrativa e supõe que com o ingresso de mais um membro nesta família aumentará proporcionalmente sua despesa semanal.

Grandezas inversamente proporcionais

Duas grandezas são inversamente proporcionais quando o aumento de uma implica na redução da outra, ou seja, quando dobramos uma delas, a outra se reduz a metade; quando triplicamos uma delas, a outra fica reduzida a terça parte, etc.

Os números racionais x, y e z são inversamente proporcionais aos números racionais a, b e c, respectivamente, quando se tem: x . a = y . b = z . c

Veja o exemplo

Razão:

12/6 = 2/1

60/120 = 1/2

Note que 12/6 e 60/120 possuem razões inversas, isto é, 2/1 é o inverso de 1/2.

Regra de três simples

Quando, em uma relação entre duas grandezas, conhecemos três valores de um problema e desconhecemos apenas um, poderemos chegar a sua solução utilizando os princípios da regra de três simples. Para isso, basta que multipliquemos os meios entre si e os extremos também entre si. Acompanhem:

Exemplo: os números 6 e 10 são diretamente proporcionais a 12 e x respectivamente. Nessas condições, vamos encontrar o valor de x que torne essa afirmação verdadeira.

Vamos à solução dos problemas (1) e (2) propostos no início deste trabalho.

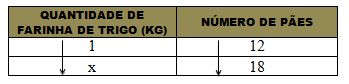
(1)          Um quilo de farinha de trigo é suficiente para fazer 12 pães. De quanta farinha necessito para fazer 18 pães?

● Vamos chamar o valor desconhecido de x emontar uma tabela contendo os valores.

Inicialmente teremos que analisar se as grandezas quantidade de farinha de trigo e número de pães são inversa ou diretamente proporcionais.

• Se duplicarmos a quantidade de farinha de trigo, a quantidade de pães também duplicará. Se triplicarmos a farinha, os pães também serão triplicados, e assim por diante. Sendo assim, somos levados a concluir que essas duas grandezas são diretamente proporcionais;
• Sabendo dessa informação, basta escrevermos a proporção de acordo com o quadro acima e partir para sua solução;
• As flechas no mesmo sentido indicam que as grandezas são diretamente proporcionais.

Conclusão: para fazer 18 pães precisaremos de 1,5 kg de farinha de trigo.

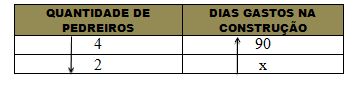
(2)   Quatro pedreiros constroem uma pequena casa em 90 dias. Dois pedreiros construirão a mesma casa em quanto tempo?

● Vamos chamar o valor desconhecido de x emontar uma tabela contendo os valores.

Como no caso anterior, teremos que analisar se as grandezas quantidade de pedreiros e dias gastos na construção são inversa ou diretamente proporcionais.

• Se aumentarmos o número de pedreiros, a duração da obra será reduzida, portanto, essas grandezas são inversamente proporcionais;
• Sabendo dessa informação, basta escrevermos a proporção de acordo com o quadro acima e partir para sua solução;
• Como as grandezas são inversamente proporcionais, devemos inverter uma das frações;
• As setas contrárias indicam que as grandezas são inversamente proporcionais.

Conclusão: se reduzirmos o número de pedreiro a dois, teremos a obra concluída em 180 dias.

Regra de três composta

Quando trabalhamos com três grandezas, direta ou inversamente proporcionais e, num determinado problema, existem seis valores, dos quais cinco são conhecidos e apenas um desconhecido, pode-se encontrar o valor da incógnita através da regra de três composta.

Vamos à solução dos problemas (3) e (4) propostos no início deste trabalho.

(3)   Se 8 homens levam 12 dias montando 16 máquinas, então, nas mesmas condições, 15 homens levarão quantos dias para montar 50 máquinas?

● Vamos chamar o valor desconhecido de x e montar uma tabela contendo os valores:

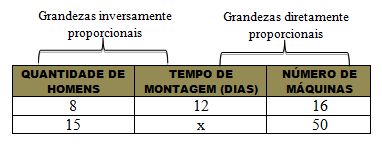Analisemos as grandezas a fim de saber se são direta ou inversamente proporcionais entre si.

• Fixando a grandeza quantidade de homens, vamos relacionar as grandezas tempo de montagem com número de máquinas. Se dobrarmos o tempo de montagem, dobraremos o número de máquinas. Logo, essas duas grandezas são diretamente proporcionais.
• Fixando a grandeza número de máquinas, vamos relacionar as grandezas quantidade de homens com tempo de montagem. Se dobrarmos o número de homens, teremos reduzido à metade o tempo de montagem. Logo, essas duas grandezas são inversamente proporcionais.
• Sabendo dessas informações, basta escrevermos a proporção de acordo com a tabela acima;
• Como temos grandezas inversamente proporcionais, devemos inverter uma das frações;

Conclusão: Com 15 homens, serão construídas 50 máquinas em 20 dias.

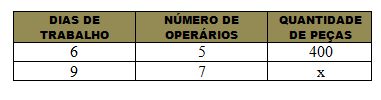
(4)   Trabalhando 6 dias, 5 operários produzem 400 peças. Quantas peças desse mesmo tipo serão produzidas por 7 operários em 9 dias de trabalho?

● Chamaremos o valor desconhecido de x:

Vamos fazer a análise dos dados contidos na tabela acima.

• Fixando a grandeza dias de trabalho, vamos relacionar as grandezas número de operários com quantidade de peças. Ao dobrarmos o número de operários, dobraremos também o número de peças fabricadas. Dessa forma, essas duas grandezas são diretamente proporcionais;
• Fixando a grandeza número de operários e relacionando as grandezas dias de trabalho com quantidade de peças, temos: ao dobrarmos o número de dias de trabalho, dobraremos também a quantidade de peças produzidas, ou seja, estas grandezas também são diretamente proporcionais;
• Portando esses dados, deveremos escrever a devida proporção de acordo com a tabela acima;
• Como temos grandezas diretamente proporcionais, manteremos as frações em suas formas originais.

Conclusão: com 7 operários, em 9 dias serão produzidas 840 peças.

“A sede de conhecimento nos faz trilhar por caminhos novos, viver aventuras, compartilhar saberes, modelar e remodelar paradigmas.”

Robison Sá.

Referências bibliográficas:

SOUZA, JOAMIR ROBERTO DE; PATARO, PATRÍCIA ROSANA MORENO. Vontade de saber matemática, 8° ano. São Paulo: FTD, 2009. – (Coleção vontade de saber)

GIOVANNI JÚNIOR, JOSÉ RUY; CASTRUCCI, BENEDICTO. – Ed. Renovada. – São Paulo: FTD, 2009. – (Coleção a conquista da matemática)

Matemática para concursos/Regra de três simples e regra de três composta. Disponível em: <http://pt.wikibooks.org/wiki/Matem%C3%A1tica_para_concursos/Regra_de_tr%C3%AAs_simples_e_regra_de_tr%C3%AAs_composta>. Acesso em: 01 de dezembro de 2012.

Regra de três. Disponível em: <http://www.slideshare.net/edigleyg3/regra-de-trs#btnPrevious>. Acesso em: 02 de dezembro de 2012.

Texto originalmente publicado em https://www.infoescola.com/matematica/regra-de-tres-simples-e-composta/