Leonhard Paul Euler foi sem dúvida um dos matemáticos mais notáveis de todos os tempos e suas contribuições para a física e a matemática ecoam até hoje. Nascido na Suíça em 15 de abril de 1707, Euler teve uma bem sucedida carreira acadêmica com contribuições e descobertas em geometria, análise matemática, teoria dos números, cálculo, lógica e foi o matemático pioneiro da Teoria dos Grafos.
Leonhard Euler. Pintura de Johann Georg Brucker.
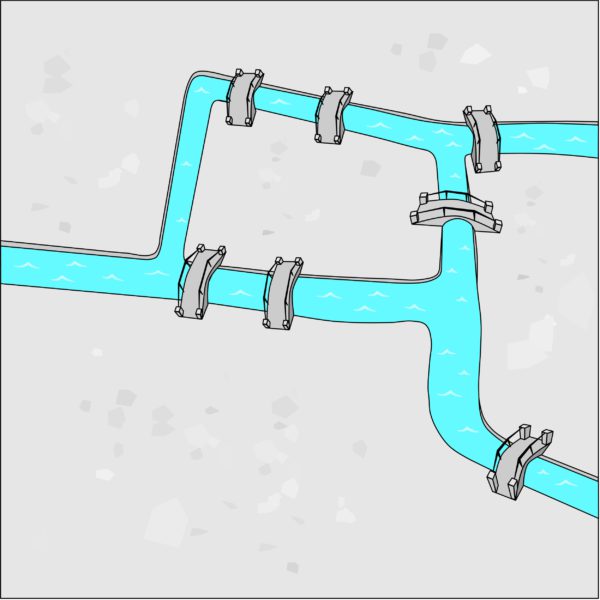
Euler publicou mais do que qualquer matemático havia feito até então, seu trabalho compreende cerca de 80 volumes. Fascinado por notações matemáticas e fórmulas, Euler define a maioria das notações usadas hoje como f(x) que indica uma função f que depende de uma variável x, a constante e que também é chamada de número de Euler, a parte imaginária i de um número complexo, o símbolo de somatório ∑ e popularizou o uso da letra grega 𝜋. Uma de suas fórmulas mais famosas, a identidade de Euler, que compreende o uso de constantes muito comuns na matemática, ficou muito conhecida, sendo nomeada por muitos a identidade mais bela da matemática:
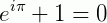
Dentre as inúmeras contribuições de Euler, destaca-se a solução do problema das pontes de Königsberg, que abriu caminho para a Teoria dos Grafos.
Ilustração das sete pontes de Königsberg. Fonte: Sergey Merkulov / Shutterstock.com
O problema enunciava: É possível cruzar cada uma das sete pontes de Königsberg uma única vez, retornando ao ponto de partida? Euler publicou a solução do problema em 1736 onde, contando as pontes ao redor de cada área provou que isto não era possível, percebendo que só seria possível atravessar o caminho inteiro passando uma única vez em cada ponte se houvesse exatamente zero ou dois pontos de onde saísse um número ímpar de caminhos. A resolução deste problema é considerado como o primeiro teorema da Teoria dos Grafos e um dos primeiros resultados topológicos da geometria.
Na física, Euler também contribuiu muito. Publicou trabalhos acerca da cinemática dos corpos, introduzindo também o teorema de Euler para os ângulos de rotação. Seu nome é citado frequentemente na mecânica, onde obteve avanços significativos no Cálculo Variacional, onde ele generaliza o princípio da mínima ação, que posteriormente tornaram-se as bases para a mecânica Lagrangiana (que é uma formulação da mecânica clássica fundamentada por Joseph-Louis Lagrange, que combina a conservação do momento linear com a conservação da energia). A Equação de Euler-Lagrange foi descoberta em meados de 1750 por Euler e Lagrange na tentativa de solucionar um problema da mecânica que consistia em encontrar uma curva no qual o tempo gasto por um objeto para deslizar sobre ela até certo ponto fosse o mínimo, independente do seu ponto de partida. Este problema também é conhecido como problema da Braquistócrona. Lagrange soluciona o problema e envia a solução para Euler que, em suas mãos, desenvolveu o método de Lagrange levando a formulação Lagrangiana da mecânica e a descoberta do cálculo das variações. Essa e outras contribuições também são devidas à Euler no campo da astronomia, ótica, mecânica dos fluidos e até na teoria musical.
Euler morre no dia 18 de setembro de 1783, aos 76 anos, devido a uma hemorragia cerebral. Instantes antes de sua morte, na mesma data, Euler discutia com seu colega Anders Lexell sobre a descoberta do planeta Urano e a sua órbita ao redor do sol, morrendo horas depois. Seu trabalho lhe garantiu o posto de um dos grandes matemáticos de todos os tempos, assim como Newton, Arquimedes e Gauss.
Referências bibliográficas:
BOYER, Carl B. História da Matemática. São Paulo: Blucher, 2012.
ROQUE, Tatiana. História da Matemática – Uma visão crítica, desfazendo mitos e lendas. São Paulo: Zahar, 2012.
ROONEY, Anne. A História da Matemática. São Paulo: M. Books do Brasil Editora, 2012.
Texto originalmente publicado em https://www.infoescola.com/biografias/leonhard-euler/