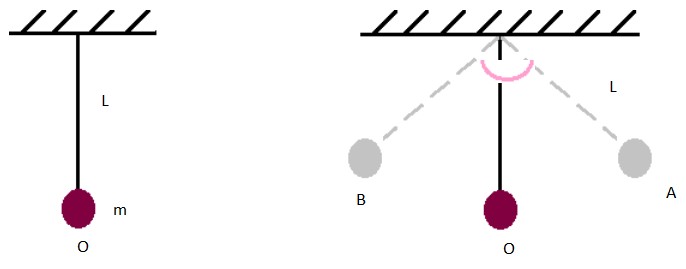
Desprezadas a resistência do ar e as demais forças dissipativas, um fio inextensível com uma massa presa a ele é um exemplo de Pêndulo Simples. Ao ser tirado de sua posição de equilíbrio O, o pêndulo realiza um movimento periódico. Ou seja, realiza o mesmo movimento (ciclo) no mesmo intervalo de tempo.
Para pequenos ângulos, o movimento de um pêndulo é considerado um MHS (movimento harmônico simples) cujo período é dado por:
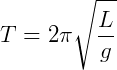
Onde:
- L é o comprimento do fio
- g é a aceleração da gravidade.
Perceba que o período do pêndulo não depende da massa presa na ponta do fio.
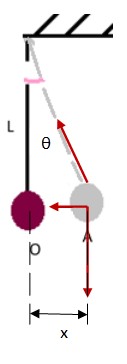
Abaixo, está a representação da força resultante F que orienta o movimento.
Na resultante, temos:
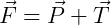
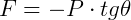
Quando o ângulo θ é pequeno, como dito, além de um MHS, o valor de sua tangente é, aproximadamente o valor do seno do ângulo. Assim:
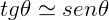
Então:
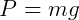
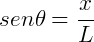
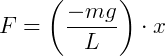
Um MHS também pode ser comparado a um sistema massa-mola em um sistema livre de forças dissipativas. Então, dada força elástica (Felást.) temos:
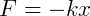
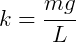
Referência:
Os Fundamentos da Física – Moderna Plus. Ramalho, Nicolau e Toledo. Vol. 01. Moderna. 11ª Ed. SP. 2016
Texto originalmente publicado em https://www.infoescola.com/fisica/pendulo-simples/