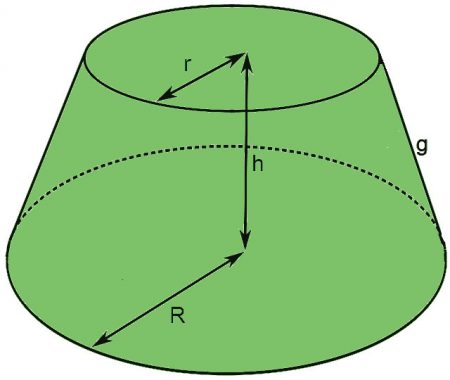
Tronco de cone

Tronco de cone de bases paralelas é um sólido obtido quando se intercepta um cone por um plano paralelo ao plano da base e se descarta o cone menor formado.

Alguns elementos do tronco de cone

• R é o raio da base maior.
• r é o raio da base menor.
• h é a altura do tronco de cone.
• g é a geratriz do tronco de cone.

É possível obtermos que é válido que: 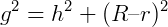$g^2 = h^2 + (R ? r)^2$

Considerando os dados indicados no tronco de cone acima, temos também que:

Volume do tronco de cone de bases paralelas (V):

$V = \frac{\pi \cdot h}{3} \cdot (R^2 + R \cdot r + r^2)$

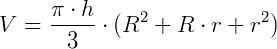
Área lateral do tronco de cone ($A_l$) de bases paralelas:

$A_l = \pi \cdot g(r+R)$

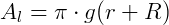
Tais expressões são obtidas pela semelhança do cone original com o cone menor criado a partir do corte feito pelo plano da definição.

Exemplo:

(FUVEST) As bases de um tronco de cone circular reto são círculos de raios de 6 cm e 3 cm. Sabendo que a área lateral do tronco é igual à soma das áreas das bases, calcule:

• a) altura do tronco de cone.
• b) volume do tronco de cone

Resposta:

a) O enunciado diz que "área lateral do tronco é igual à soma das áreas das bases". Sendo A₁ e A₂ as áreas dos círculos da base de raios 6 cm (R) e 3 cm (r), respetivamente. Temos:

$A_1 + A_2 = A_l$

$A_1 = \pi R^2 = \pi 6^2 = 36\pi$

$A_2 = \pi r^2 = \pi 3^2 = 9\pi$

$A_l = A_1 + A_2 = 36\pi + 9\pi = 45\pi$

$A_l = \pi \cdot g(r+R) = \pi \cdot g(3+6) = \pi \cdot g \cdot 9$

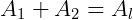
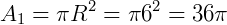
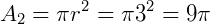
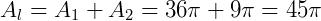
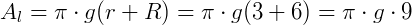
Logo: 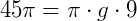$45\pi = \pi \cdot g \cdot 9$.

Portanto: g = 5 cm

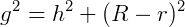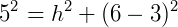
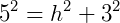
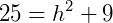
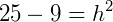
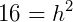
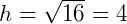
Pede-se a altura do tronco de cone (h), para isso, utilizamos a relação $g^2 = h^2 + (R - r)^2$:

$5^2 = h^2 + (6-3)^2$

$5^2 = h^2 + 3^2$

$25 = h^2 + 9$

$25 - 9 = h^2$

$16 = h^2$

$h = \sqrt{16} = 4$

Portanto, h = 4 cm.

b) Temos que h = 4 cm, R = 6 cm e r = 3 cm. Basta usar a expressão para volume:

$V = \frac{\pi \cdot h}{3} \cdot (R^2 + R \cdot r+r^2)$

$V = \frac{\pi \cdot 4}{3} \cdot (6^2 + 6 \cdot 3+3^2)$

$V = \frac{4\pi}{3} \cdot (36+18+9)$

$V = \frac{4\pi \cdot 63}{3}$

$V = 84 \pi cm^3$

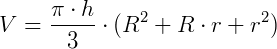
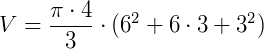
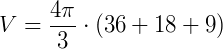
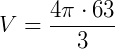
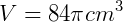
Texto originalmente publicado em https://www.infoescola.com/geometria-espacial/tronco-de-cone/