Aplicações das Equações Diferenciais

Equações diferenciais são ferramentas importantes para diversos ramos das ciências exatas. Com elas é possível descrever e formular diversos tipos de sistemas físicos numa linguagem matemática, o que possibilita uma imensa gama de aplicações em modelos concretos. Nesse artigo veremos algumas das suas aplicações.

Decaimento Radioativo

Na física atômica, o decaimento radioativo é bem definido usando EDOs. A medida de estabilidade de um determinado elemento é chamada de meia-vida. A meia-vida de um elemento é simplesmente o tempo necessário para que metade dos átomos de uma quantidade inicial N₀ se desintegre ou se transforme em átomos de outro elemento. Quanto maior a meia-vida de um elemento, mais estável ela é. Por exemplo, o isótopo de Urânio U-238 possui meia vida de 4,5 bilhões de anos, ou seja, metade de uma quantidade desse isótopo será transmutada em Chumbo Pb-206. Vejamos abaixo um estudo sobre o decaimento do U-238 usando EDO.

1) Um reator converte Urânio 238 em isótopo de Plutônio 239. Após 15 anos, foi detectado que 0,043% da quantidade inicial N₀ de Plutônio se desintegrou. Vamos encontrar a meia-vida desse isótopo, dada a taxa de desintegração que é proporcional à quantidade remanescente.

Seja N(t) a quantidade de Plutônio remanescente num instante 𝑡. Usando a solução para um problema de valor inicial onde:

$\frac{dN\left(t\right)}{\mathit{dt}}=\mathit{kN},N\left(0\right)={N}_{0}$

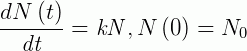
É dada por:

$N\left(t\right)={N}_{0}{e}^{\mathit{kt}}$

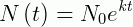
Como enunciado, 0,043% dos átomos da quantidade 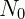${N}_{0}$ se desintegrou, então nos resta 99,957% do elemento. Para calcularmos o valor de k usamos:

${N\left(15\right)=N}_{0}{e}^{15k}={\mathrm{0,99957}N}_{0}$

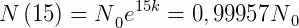
Resolvendo, temos:

${{N}_{0}e}^{15k}={\mathrm{0,99957}N}_{0}$

${e}^{15k}=\mathrm{0,99957}$

$15k=\ln \left(\mathrm{0,99957}\right)$

$k=\frac{\ln \left(\mathrm{0,99957}\right)}{15}=-\mathrm{0,00002867}$

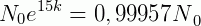
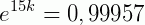
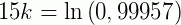
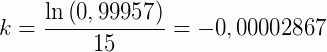
Encontrando então o valor da constante k. Agora, substituindo na equação:

${N\left(t\right)=N}_{0}{e}^{\left(-\mathrm{0,00002867}\right)t}$

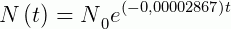
Como a meia-vida é dado pelo instante onde:

$N\left(t\right)=\frac{{N}_{0}}{2}$

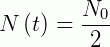
Então, vamos calcular o valor de 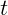$t$na equação acima:

$\frac{{N}_{0}}{2}={N}_{0}{e}^{\left(-\mathrm{0,00002867}\right)t}$

$\frac{1}{2}={e}^{\left(-\mathrm{0,00002867}\right)t}$

$t=\frac{\ln 2}{\mathrm{0,00002867}}=\mathrm{24.176,74}\mathit{anos}$

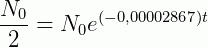
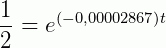
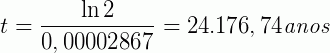
Crescimento de uma Colônia de Bactérias

Em uma colônia de bactérias com população inicial de 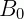${B}_{0}$bactérias, foi observado uma hora depois (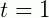$t=1$) que o número de bactérias passou a ser 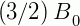${\left(3/2\right)B}_{0}$. Se a taxa de crescimento é proporcional ao número de bactérias numa amostra, vamos determinar o tempo necessário para que o número de bactérias seja o triplo do valor inicial. Dado o PVI:

$\frac{dB\left(t\right)}{\mathit{dt}}=kB,B\left(0\right)={B}_{0}$

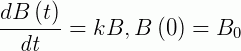
E usando a condição:

${B\left(1\right)=\frac{3}{2}B}_{0}$

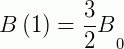
Devemos primeiramente encontrar o valor da constante k.

$\frac{dB\left(t\right)}{\mathit{dt}}-\mathit{kB}=0$

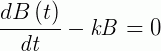
Multiplicando o fator de integração em ambos os lados da equação, obtemos a expressão:

$\frac{d}{\mathit{dt}}\left\lbrack {e}^{-\mathit{kt}}B\right\rbrack =0$

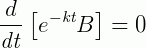
E derivando, obtemos:

${e}^{-\mathit{kt}}B=C\rightarrow B\left(t\right)={Ce}^{\mathit{kt}}$

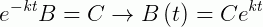
Como temos interesse em descobrir o valor de k no instante t=1, fazemos:

${{{B}_{0}e}^{k}=\frac{3}{2}B}_{0}$

$k=\ln \left(\frac{3}{2}\right)=\mathrm{0,4055}$

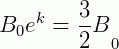
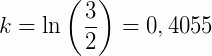
Obtendo assim, a expressão:

${B\left(t\right)=B}_{0}{e}^{\mathrm{0,4055}t}$

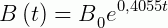
Como queremos encontrar o tempo necessário para que o número de bactérias seja triplicado, fazemos:

${3{B}_{0}={B}_{0}e}^{\mathrm{0,4055}t}$

$t=\frac{\ln 3}{\mathrm{0,}4055}\approx \mathrm{2,71}\mathit{horas}$

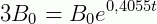
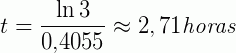
Referências bibliográficas:

ZILL, Dennis G. Equações Diferenciais Com Aplicações em Modelagem. São Paulo – Cengage Learning, 2016.

BASSALO, José Maria FIlardo; CATTANI, Mauro Sérgio Dorsa. Elementos de Física Matemática – Volume 1. São Paulo – Livraria da Física, 2010.

ARFKEN, George B; WEBER, Hans J; HARRIS, Frank E. Física Matemática: Métodos Matemáticos para Engenharia e Física – 7a Ed. Rio de Janeiro: Elsevier, 2017.

Texto originalmente publicado em https://www.infoescola.com/matematica/aplicacoes-das-equacoes-diferenciais/