Área de polígonos regulares

Polígonos são figuras geométricas planas que são formadas por segmentos de reta a partir de uma sequência de pontos de um plano, todos distintos e não colineares, onde cada extremidade de qualquer um desses segmentos é comum a apenas um outro.

Um polígono convexo é regular quando seus lados são todos iguais (possuem a mesma medida) e seus ângulos internos também são iguais.

Na geometria plana, existem diferentes tipos de polígonos e, para muitos deles, há uma fórmula matemática para se calcular sua área.

Área de um triângulo regular

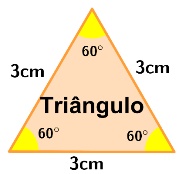
Um triângulo regular é também chamado de triângulo equilátero. Obtemos a sua área através da seguinte fórmula matemática: 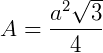$A = \frac{a^2 \sqrt{3}}{4}$.

Onde a é a medida do lado do triângulo. Obtemos essa fórmula da seguinte maneira:

Considere o triângulo regular ABC, de lado a:

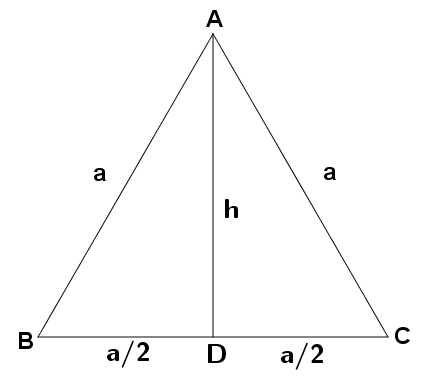
Vamos nos concentrar em um dos triângulos retângulos que foram formados, ABD e aplicar o Teorema de Pitágoras.

$a^2 = h^2 + \left(\frac{a}{2}\right)^2$

$a^2 = h^2 + \frac{a^2}{4}$

$h^2 = a^2 - \frac{a^2}{4}$

$h^2 = \frac{3a^2}{4}$

$h = \sqrt{\frac{3a^2}{4}}$

$h = \frac{a\sqrt{3}}{2}$

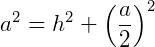
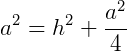
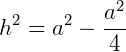
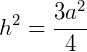
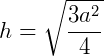
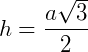
Agora, como a área de um triângulo qualquer é: 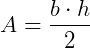$A = \frac{b \cdot h}{2}$, teremos:

$A = \frac{a \cdot \left(\frac{a \sqrt{3}}{2}\right)}{2} = \frac{a^3\sqrt{3}}{2} \cdot \frac{1}{2} = \frac{a^3\sqrt{3}}{4}$

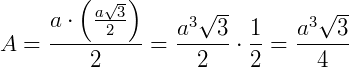
Assim, em todo triângulo regular encontramos a sua área utilizando a fórmula 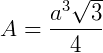$A = \frac{a^3\sqrt{3}}{4}$.

Área de um quadrado

Um quadrado, por si só, já é regular pois, por definição, é um quadrilátero cujos lados são sempre iguais.

Calculamos a sua área multiplicando a sua base pela sua altura:

$A = b \cdot h$

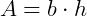
Área de um hexágono regular

Vamos considerar um hexágono regular de lado L e apótema a.

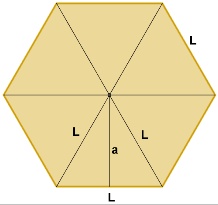
O hexágono é o único polígono regular onde todos os seus 6 triângulos são também regulares (equiláteros).

Assim, para calcular a área de um dos triângulos basta utilizar a fórmula: 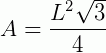$A = \frac{L^2\sqrt{3}}{4}$.

Como temos 6 triângulos que formam o hexágono, a sua área será, então:

$A = 6 \cdot \frac{L^2\sqrt{3}}{4} = 3 \cdot \frac{L^2\sqrt{3}}{2}$

$A = \frac{3L^2 \sqrt{3}}{2}$

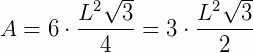
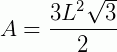
Fórmula geral para cálculo da área de qualquer polígono regular

Existe uma fórmula que nos dá a área de qualquer polígono regular. A fórmula é a seguinte:

$A = \frac{n \cdot L \cdot a}{2}$

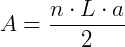
Onde n é a quantidade de lados do polígono, L é a medida do lado desse polígono e a é a medida do apótema, quase sempre dado.

Para chegarmos à fórmula, vamos considerar o hexágono abaixo e suponhamos que não sabemos da existência de uma fórmula específica pra ele (como vimos anteriormente).

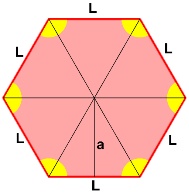
Um hexágono é um polígono regular de 6 lados. Podemos dividir esse polígono em 6 triângulos idênticos. Assim, para determinar a área desse hexágono, basta determinar a área de um dos triângulos e, em seguida, multiplicar o resultado por 6.

A área de um triângulo qualquer é calculada multiplicando-se a sua base pela sua altura e dividindo esse resultado pela metade, ou seja, 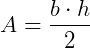$A = \frac{b \cdot h}{2}$.

No caso desse hexágono, a base do triângulo em destaque será L e a altura será a, que é o apótema do hexágono.

O apótema é a medida do segmento que parte do centro do polígono e forma ângulo de 90° com um de seus lados. Nesse caso, o apótema a desse polígono tem a mesma medida que a altura do triângulo em destaque.

Assim, a área será: 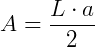$A = \frac{L \cdot a}{2}$.

Como o hexágono é composto por 6 triângulos iguais ao destacado, para encontrar a área do hexágono, devemos multiplicar a área do triângulo por 6: 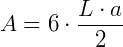$A = 6 \cdot \frac{L \cdot a}{2}$.

Veja que, se fosse um polígono de 5 lados, teríamos 5 triângulos e, por isso, multiplicaríamos a área do triângulo por 5. O mesmo aconteceria com um polígono regular de 10 lados: teríamos 10 triângulos e a área seria multiplicada por 10.

Considerando, então, um polígono de n lados, teríamos n triângulos iguais e a área deveria ser multiplicada por n. Assim, 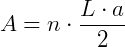$A = n \cdot \frac{L \cdot a}{2}$.

Observe que, ajeitando a fórmula para 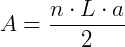$A = \frac{n \cdot L \cdot a}{2}$, temos que 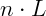$n \cdot L$ é, na verdade, o perímetro do polígono. Como o perímetro é a soma de todos os lados e temos n lados iguais a L, o perímetro será 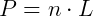$P = n \cdot L$. Assim, também podemos expressar essa fórmula como:

$A = \frac{P \cdot a}{2}$

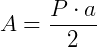
Se a medida do apótema não for dada, teremos que o encontrá-la.

Apótema

Para calcular o apótema vamos considerar um polígono regular de 6 lados, um hexágono, cujo lado mede 3 cm.

$\frac{360^o}{6} = 60^o$

$\frac{60^o}{2} = 30^o$

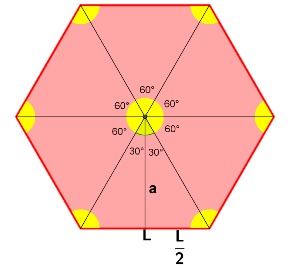
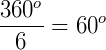
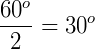
Primeiro precisamos saber qual será o ângulo no ponto de onde sai o apótema. Para isso, pasta dividir 360° pela quantidade de lados do polígono, no nosso caso, 6 lados. Assim, teremos 60°.

O apótema sempre divide o ângulo em dois outros ângulos de mesma medida, no nosso caso, 30°. Agora, podemos usar algumas relações trigonométricas para encontrar o valor do apótema:

$tg(30^o) = \frac{\text{cateto oposto}}{\text{cateto adjacente}}$

$tg(30^o) = \frac{\frac{L}{2}}{a}$

$a \cdot tg(30^o) = \frac{L}{2}$

$a = \frac{L}{2 \cdot tg(30^o)}$

$a = \frac{3}{2 \cdot \frac{\sqrt{3}}{3}} = 3 \cdot \frac{3}{2 \cdot \sqrt{3}} = \frac{9}{2 \cdot \sqrt{3}}$

$a = \frac{9}{2 \sqrt{3}} \cdot \frac{sqrt{3}}{\sqrt{3}} = \frac{9 \sqrt{3}}{2 \cdot 3} = \frac{3 \sqrt{3}}{2}$

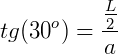
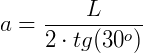
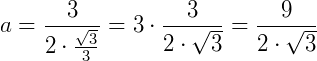
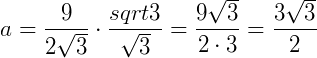
Generalizando para o caso onde temos um polígono de lado n lados de medida L:

O ângulo do apótema será dado por 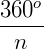$\frac{360^o}{n}$. Como temos que dividir esse ângulo por 2, teremos: $\frac{\frac{360^o}{n}}{2} = \frac{360^o}{n} \cdot \frac{1}{2} = \frac{180^o}{n}$.

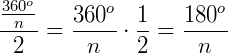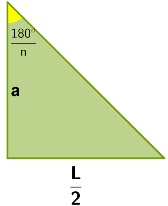
Aplicando trigonometria para encontrar o apótema:

$tg(\frac{180^o}{n}) = \frac{\frac{L}{2}}{a}$

$a \cdot tg(\frac{180^o}{n}) = \frac{L}{2}$

$a = \frac{L}{2 \cdot tg(\frac{180^o}{n})}$

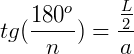
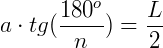
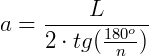
Com essa fórmula do valor do apótema, a nossa fórmula 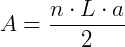$A = \frac{n \cdot L \cdot a}{2}$ pode ser escrita como:

$A = \frac{n \cdot L \cdot \left(\frac{L}{2 \cdot tg \left(\frac{180^o}{n}\right)}\right)}{2} = \frac{\frac{n \cdot L \cdot L}{2 \cdot tg \left(\frac{180^o}{n}\right)}}{2} = \frac{nL^2}{2tg \left(\frac{180^o}{n}\right)} \cdot \frac{1}{2}$

$A = \frac{nL^2}{4tg \left(\frac{180^o}{n}\right)}$

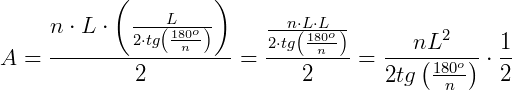
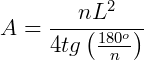
Essa é a fórmula geral para se calcular a área de qualquer polígono regular.

Exemplos

1. Qual a área de um polígono regular de 12 lados, onde cada lado mede 4 cm?

Aplicando a fórmula obtida teremos:

$A = \frac{nL^2}{4tg \left(\frac{180^o}{n}\right)}$

$A = \frac{12 \cdot 4^2}{4tg \left(\frac{180^o}{12}\right)}$

$A = \frac{12 \cdot 16}{4tg \left(15^o\right)}$

$A = \frac{192}{4 \cdot \left(2 - \sqrt{3} \right)}$

$A = \frac{48}{2 - \sqrt{3}}$

$A = 179,13 cm^2$

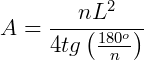
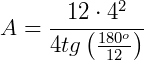
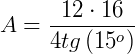
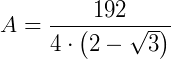
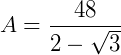
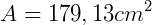
2. Qual a área de um polígono regular de 4 lados, que tem 6 como medida de cada lado?

Temos um quadrado de lado 6, cuja área pode ser calculada por:

$A = L^2 = 6^2 = 36 cm^2$

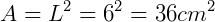
Mas vamos calcular utilizando a fórmula obtida anteriormente:

$A = \frac{nL^2}{4tg \left(\frac{180^o}{n}\right)}$

$A = \frac{4 \cdot 6^2}{4tg \left(\frac{180^o}{4}\right)}$

$A = \frac{4 \cdot 36}{4tg \left(45^o \right)}$

$A = \frac{36}{1} = 36cm^2$

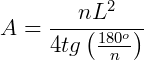
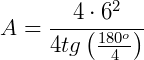
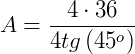
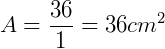
O que nos mostra a validade da fórmula.

Referências:

DOLCE, Osvaldo; POMPEO, José Nicolau. Fundamentos de Matemática Elementar. Geometria Plana. Vol. 9. São Paulo: Atual, 1995.

RIBEIRO, Paulo Vinícius. Matemática: Áreas de polígonos. Vol. 5. São Paulo: Bernoulli.

Texto originalmente publicado em https://www.infoescola.com/matematica/area-de-poligonos-regulares/