Área externa de sólidos geométricos

Suponha que exista uma caixa em formato de cubo (Figura 1) e que você irá desmontá-la (Figura 2):

Figura 1	Figura 2

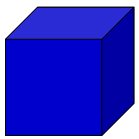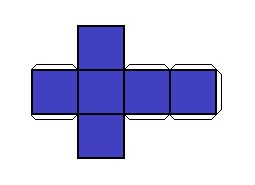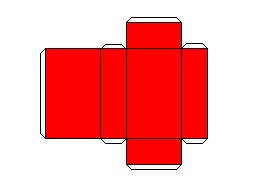
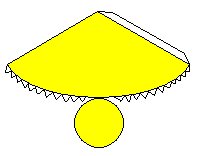
Repare que houve uma transformação de um objeto de três dimensões (3D) para um objeto de duas dimensões (2D). Tal processo chamamos, em Matemática, de Planificação. Veja mais algumas planificações abaixo:

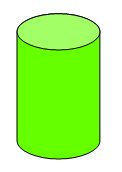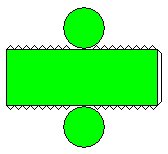O volume de um sólido geométrico é a medida da região de espaço tridimensional limitada por sua superfície. A superfície, por sua vez, torna-se uma figura plana através da planificação, como vimos acima. A área externa de um sólido geométrico é a área da superfície desse sólido.

Veja abaixo expressões de área externa de alguns sólidos.

Cubo

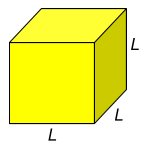
Cubo de arestas medindo L.

Expressão da área externa do cubo: 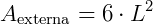$A_\text{externa} = 6 \cdot L^2$

Paralelepípedo

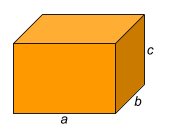
Paralelepípedo de comprimento a, largura b e altura c.

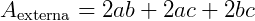
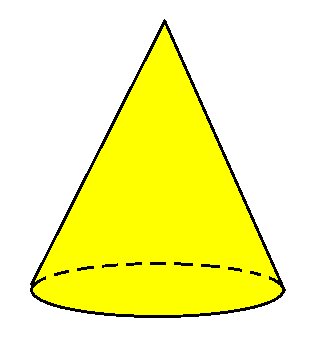
Expressão da área externa do paralelepípedo: $A_\text{externa} = 2ab + 2ac + 2bc$

Cone

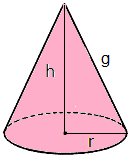
Cone reto de raio da base r, altura h e g de modo que g² = r² + h².

Expressão da área externa do cone: 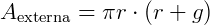$A_\text{externa} = \pi r \cdot (r+g)$

Cilindro

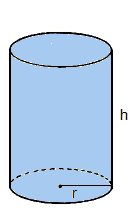
Cilindro reto de raio da base r e altura h.

Expressão da área externa do cilindro: 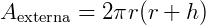$A_\text{externa} = 2\pi r (r+h)$

Esfera

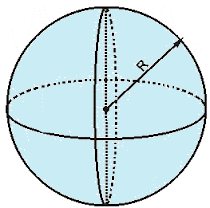
Esfera de raio R.

Expressão da área externa da esfera: 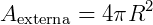$A_\text{externa} = 4\pi R^2$

Texto originalmente publicado em https://www.infoescola.com/matematica/area-externa-de-solidos-geometricos/