Resumo
Esse trabalho visa mostrar as principais ideias sobre os conjuntos e suas múltiplas ferramentas auxiliadoras do ensino-aprendizagem da matemática. Abordam-se os conceitos históricos mais relevantes e as propriedades algébricas típicas desse campo do saber. O apreciador desse trabalho visualizará uma introdução fiel aos preceitos históricos e operatórios desenvolvidos ao longo do tempo por grandes matemáticos como George Cantor e Richard Dedekind.
Conteúdo deste artigo
Conceitos históricos
Conjunto é toda coleção de elementos reunidos por meios de propriedades, regras ou características comuns, sejam formados por elementos matemáticos ou de qualquer área do conhecimento humano. A Teoria dos Conjuntos trata somente de coleções de elementos proeminentes ou pertinentes à matemática. As ideias sobre conjuntos dominam os campos matemáticos e são à base da nova linguagem da matemática e indispensável a qualquer outra ramificação da meta ciência estudada nos meios científicos e educacionais.
Um pouco de atenção é necessária quando se quer abordar os conteúdos relacionados aos conjuntos. Muitos autores, até mesmo renomados, usam a nomenclatura incorreta em seus livros, nesse tópico específico, batizando esse assunto básico como a Teoria dos Conjuntos. A teoria dos conjuntos existe, mas nessa fase da aprendizagem, ensino fundamental ou médio, o estudante apenas estuda uma introdução deste tópico, ficando para abordagens futuras, – ensino superior - o conhecimento sobre conjuntos em todas as suas minúcias e complexidade.
Desde tempos remotos, especificamente no século V a.C., matemáticos de prestígio buscavam a compreensão sobre o infinito. Exemplo disso foi o matemático grego Zenão, bem como os matemáticos indianos. Mas, a compreensão moderna que se tem sobre o infinito, as grandes descobertas nesse campo, data de um período entre 1867 e 1871. Foi nessa época, através dos matemáticos George Cantor e Richard Dedekind, especialmente em 1870, que se pôde entender detalhadamente os conceitos sobre o infinito, operações, reciprocidade entre elementos e conjuntos e outras diversas descobertas que acabaram revolucionando os conhecimentos matemáticos nesse campo de pesquisa.
As ideias iniciais sobre conjuntos são dadas ainda no ensino fundamental e expandidas no ensino médio. Esse conhecimento serve de alicerce para todos os campos matemáticos dando-lhes possibilidades de cálculos, generalizações, facilitações de linguagens e aplicabilidades cotidianas. Toda matemática moderna é sustentada na concepção de Conjuntos.
Todos os grandes temas de debates matemáticos surgem do fervor das discussões entre seus pesquisadores. Bem, com Cantor foi diferente. Ele, por si só, e de uma única vez, lançou um artigo que contemplou todas as discussões relacionadas às ideias sobre os conjuntos. Esse artigo foi publicado em 1874 e tinha como título “A respeito de uma propriedade característica de todos os números reais”. De início o trabalho recém-lançado por Cantor fragmentou os matemáticos da época. Em sua defesa estavam Karl Weierstrass e Dedekind e no lado oposto estava Leopold Kronecker, em dias atuais, conhecido como o criador do construtivismo matemático.
Tempos depois, matemáticos dedicados ao estudo dos conjuntos, descobriram que nas teorias cantorianas existiam várias contradições. Por volta de 1900 foi descoberto o principal dos paradoxos da Teoria dos Conjuntos, o paradoxo de Russell, que leva esse nome em homenagem a um dos seus descobridores, Bertrand Russell. Foram Russell e Ernst Zermelo, quem descobriram este que é um dos paradoxos mais famosos da história da humanidade: “o conjunto de todos os conjuntos que não são membros de si mesmos”.
Atualmente, existem várias formas de expressar um conjunto, seja através de uma propriedade comum a todos os seus elementos, do diagrama de Venn (matemático e lógico inglês, 1834-1923), dos diagramas de Euller (matemático e físico suíço, 1707-1783) ou nomeando os seus elementos. Um dos motivos pelo qual se considera imprescindível trabalhar com conjuntos, é que implicitamente, existe uma álgebra capaz de operar com união, interseção, diferença, além das propriedades comutativa e distributiva e outras possibilidades mais que sem essa linguagem seria impossível realizar.
Representando um conjunto e seus elementos
Podemos representar um conjunto de diversas formas por meio de ferramentas desenvolvidas ao longo do tempo por investigadores matemáticos engajados na busca por mecanismos facilitadores da compreensão sobre os conjuntos e suas aplicações. Confira essas ferramentas: diagrama de Venn, propriedade comum a todos os elementos ou simplesmente nomeando-o.
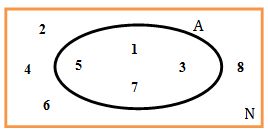
O diagrama de Venn consiste em escrever os elementos na parte interna de uma região circular, não necessariamente regular, convexa.
O conjunto A é formado pelos elementos 1, 3, 5 e 7, eles estão dentro do diagrama de Venn. Já os elementos 2, 4, 6 e 8 estão dentro do conjunto dos números naturais N, mas não fazem parte do conjunto A.
Podemos representar os conjuntos acima por meio de uma propriedade que seja comum a todos os elementos de cada um deles. Confiram:
- A é o conjunto dos números ímpares menores que 9.
- N é o conjunto dos números naturais menores que 9.
Outra possibilidade de expressarmos esses conjuntos é simplesmente nomeando-os. Acompanhem:
- A = {1, 3, 5, 7}
- N = {1, 2, 3, 4, 5, 6, 7, 8}
Para nomear um conjunto utilizamos letras maiúsculas do alfabeto latino: A, B, C, D,... Z.
Para nomear elementos genéricos de um conjunto utilizamos as letras minúsculas do alfabeto latino: a, b, c, d,... z.
Quando quisermos representar um conjunto por meio da escrita dos seus elementos, é necessário que os coloquemos entre chaves e os separemos por vírgulas. Vejam:
C = {b, c, d, f} F = {a, e, i, o, u}
Conjuntos especiais
São vários os tipos de conjuntos, mas entre eles, dois são caracterizados como especiais devido as suas especificidades. São eles o vazio e o unitário.
O Conjunto Vazio é caracterizado pela ausência de elementos. Verifiquem como podem ser feitas as suas representações:
V = { } V = Ø V = { x/ x ≠ x}
Observação: jamais deveremos representar o conjunto vazio como V = {Ø}, pois isso significa que este conjunto contém um elemento Ø tornando-o unitário.
O Conjunto Unitário possui apenas um elemento.
M = {u} M = {Ø}
Relação de pertinência
Entre os elementos de um conjunto e este próprio conjunto existe uma relação digna de atenção. Um elemento pode pertencer ou não a um conjunto. Se pertence usamos o símbolo ∈, se não, usamos o símbolo ∉.
- Dado o conjunto F = {a, d, e, g}, temos que a ∈ F, e ∈ F, porém t ∉ F e m ∉ F.
Observação: elementos pertencerão ou não a um determinado conjunto. Um elemento não poderá, jamais, estar contido num conjunto.
Relação de inclusão
Há também uma relação importante encontrada ao se observar alguns conjuntos. Um conjunto A estará contido em outro conjunto B caso todos os elementos de A pertençam também a B. A esta relação damos o nome de inclusão de conjuntos. Veja como representamos essa relação simbolicamente:
- A ⊂ B : A está contido em B; B contém A ou A é subconjunto de B.
- A ⊄ B : A não está contido em B; B não contém A ou A não é subconjunto de B. Nesse caso dizemos que os conjuntos A e B são disjuntos.
Exemplo: dados os conjuntos M = {2, 3, 5, 7} e N = {x/ x é primo}, temos que M ⊂ N, pois todo elemento de M é também elemento de N.
Regras básicas
Por trás da linguagem dos conjuntos existe uma álgebra que nos permite operar com mais facilidade sobre os conteúdos matemáticos. Destacam-se aqui as três principais propriedades algébricas a fim meramente de ilustrar as possibilidades abertas pelo conhecimento sobre os conjuntos.
- Reflexiva: A ⊂ A;
- Antissimétrica: se A ⊂ B e B ⊂ A então A = B;
- Transitiva: se A ⊂ B e B ⊂ C então A ⊂ C.
Considerações finais
Muito mais há sobre a linguagem, representação e propriedades dos conjuntos. O objetivo deste trabalho foi mostrar alguns dos tópicos básicos relacionados a este campo tão vasto da matemática que com certeza não seria possível abranger nas poucas linhas de um artigo. Existem várias outras propriedades algébricas possíveis de se realizar utilizando a linguagem dos conjuntos. Várias delas advêm das relações entre conjuntos e não foram abordadas por conveniência, nesse texto. São elas: união, interseção, diferença, complementar e todas as suas ramificações.
A linguagem dos conjuntos nos proporciona um ambiente vasto de ferramentas facilitadoras do aprendizado da matemática, portanto, devemos nos dedicar a abstração desse saber ímpar e propagador de novos saberes matemáticos.
“Somos elementos de um conjunto vivo, ascendente e propagador de amores chamado família”.
Robison Sá.
Referências bibliográficas:
LIMA, ELON LAGES. A matemática do ensino médio – volume 1 - 9. ed. – Rio de Janeiro: SBM, 2006. 237p.
MORI, IRACEMA; ONAGA, DULCE SATIKO. Matemática: ideias e desafios – 6ª série – 14. ed. São Paulo: saraiva, 2005. 303p.
Teoria dos conjuntos. Disponível em: http://pt.wikipedia.org/wiki/Teoria_dos_conjuntos. Acesso em: 15 de setembro de 2012.
Texto originalmente publicado em https://www.infoescola.com/matematica/conjuntos-uma-abordagem-introdutoria/