Funções exponenciais são ferramentas muito importantes para a matemática devido ao número imenso de aplicações que ela nos proporciona. Alguns estudos que fazem uso desse tipo de funções são aqueles envolvendo cálculos financeiros,datação por carbono-14 de minerais e artefatos arqueológicos, crescimento de bactérias e populacional e muitas outras aplicações práticas. Sendo assim, vamos às definições: Seja uma função 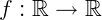 e 𝑎, uma constante real. Essa função é chamada de exponencial se a lei de associação puder ser escrita da forma:
e 𝑎, uma constante real. Essa função é chamada de exponencial se a lei de associação puder ser escrita da forma:
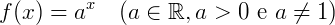
Obs.: Para melhor compreensão do conteúdo, é recomendado que o leitor revise as definições de funções matemáticas e de equações exponenciais.
Gráfico de uma função exponencial
A função exponencial admite duas interpretações do seu gráfico:
a > 1 - Estritamente crescente
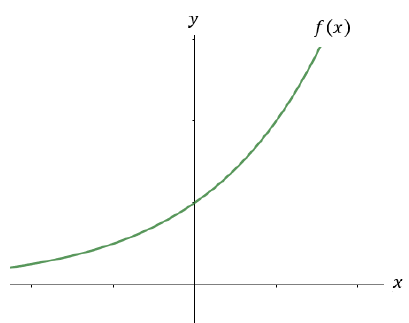
0 < a < 1 – Estritamente decrescente
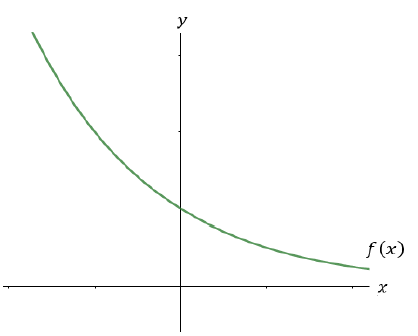
Funções exponenciais de base e
É uma função exponencial onde a base é a constante de Euler, ou simplesmente e. A sua forma será:
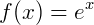
Aplicações:
Vejamos agora alguns exercícios práticos envolvendo funções exponenciais:
1) O número de bactérias de uma certa cultura pode ser previsto pela função:
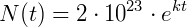
Onde k é uma constante positiva e t é o tempo dado em dias. O número inicial de bactérias aumentou 100 vezes em 2 dias, qual será o número de bactérias após 30 dias?
Vamos solucionar este problema da seguinte maneira: Considere que um número inicial de bactérias possa ser chamado de N0 e esse número foi calculado no tempo t=0. Sendo assim:
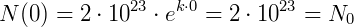
Como o problema nos diz que o número de bactérias aumentou 100 vezes em relação a N0 num tempo 𝑡=2, temos, resolvendo a equação exponencial:
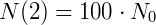
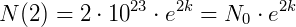

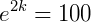
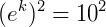
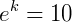
Agora, as nossas constantes já foram calculadas, o que resulta na função exponencial:
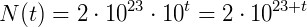
Como o exercício pede, o número de bactérias num tempo 𝑡 = 30, então:
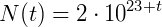
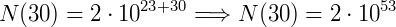
Resultando então em 2 ∙ 1053 bactérias num espaço de 30 dias.
2) Chamamos de montante (𝑀) a quantia que uma pessoa deve receber após aplicar um capital (𝐶), a juros compostos, a uma taxa (𝑖) durante um tempo (𝑡). O montante é calculado segundo a formula:
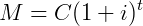
Supondo que o capital aplicado foi de R$ 200.000,00 a uma taxa de 12% ao ano durante 3 anos, qual será o montante no final da aplicação?
Para calcular este problema basta substituir pelos valores dados, mas atenção ao valor da taxa, que está em porcentagem, neste caso podemos dizer que:
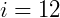
Voltando, temos:
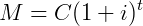
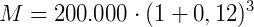
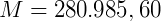
Referências Bibliográficas
GUIDORIZZI, Hamilton L. Um Curso de Cálculo: Volume 1. Rio de Janeiro: Editora LTC,2001.
DEMANDA, Franklin D; WAITS, Bert K.; FOLEY, Gregory D.; KENNEDY, Daniel. Pré Calculo. São Paulo: Pearson, 2013.
Texto originalmente publicado em https://www.infoescola.com/matematica/funcao-exponencial/
