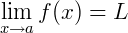Para calcularmos limites de funções é necessário recordarmos a definição formal de limites e também o conceito de continuidade de funções (ler o artigo sobre limites); então, a definição formal de limites nos diz:
Seja 𝑓 uma função e 𝑎 um ponto contido no domínio de 𝑓. Dizemos que 𝑓 tem limite 𝐿, no ponto 𝑎, se dado qualquer 𝜀 > 0, exista um 𝛿 > 0 tal que, para qualquer 𝑥 pertencente ao domínio de 𝑓, a condição abaixo seja satisfeita:
0 < |𝑥 − 𝑎| < 𝛿 ⇒ |𝑓(𝑥) − 𝐿| < 𝜀
O limite L, quando existe, é único e representamos por:
Se combinarmos a definição de continuidade e de limites podemos simplesmente dizer que, se uma função 𝑓(𝑥) é contínua em 𝑎, então:
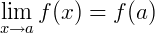
Vamos, primeiramente, introduzir algumas propriedades úteis para calcular limites de funções:
1) Considere duas funções 𝑓(𝑥) e 𝑔(𝑥) onde queremos calcular o limite da soma de ambas. Neste caso, o limite da soma é a soma dos limites, ou seja:
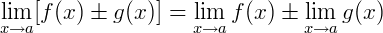
Exemplo 1: Vamos calcular o limite de 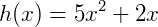 tendendo a 1:
tendendo a 1:
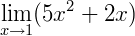
Note que a função poder ser escrita como a soma de duas outras, onde 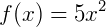 e
e 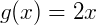 . Como ambas são contínuas num ponto 𝑎 qualquer que, neste caso, é igual a 1, temos:
. Como ambas são contínuas num ponto 𝑎 qualquer que, neste caso, é igual a 1, temos:
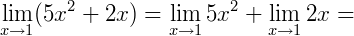
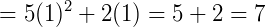
Logo, o limite da função no ponto 𝑥 = 1 vale 7, em outras palavras, 7 é o valor que 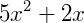 deveria ter em 1 para ser contínua nesse ponto.
deveria ter em 1 para ser contínua nesse ponto.
2) Seguinte a mesma lógica, se uma função é escrita pelo produto de duas outras, então vale a propriedade:
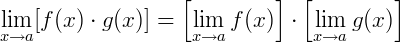
Ou seja, o limite do produto, é o produto dos limites.
3) Se uma função é obtida pela razão de duas outras, então vale:
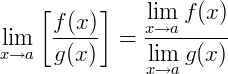
4) Se quisermos calcular o limite de uma função constante do tipo 𝑓(𝑥) = 𝑘, o seu limite será a própria constante:
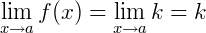
5) As funções do tipo 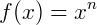 e
e 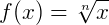 são contínuas para qualquer valor de 𝑛 pertencente aos naturais e maior do que 1 (∀𝑛 ≥ 1 , 𝑛 ∈ ℕ). Logo, podemos calcular o limite de funções desse tipo segundo a regra:
são contínuas para qualquer valor de 𝑛 pertencente aos naturais e maior do que 1 (∀𝑛 ≥ 1 , 𝑛 ∈ ℕ). Logo, podemos calcular o limite de funções desse tipo segundo a regra:
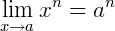

Muitas vezes, para calcularmos limites de funções, utilizar técnicas de fatoração podem nos ajudar a poupar tempo. Vejamos:
Exemplo 2: Vamos calcular:
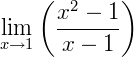
Note que se quiséssemos calcular este limite seguindo a regra número 3, encontraríamos uma indeterminação, pois a função não é contínua no ponto 𝑥 = 1,veja o porquê:
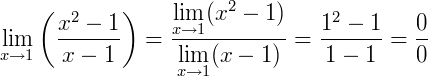
O quociente 0/0 é indeterminado. Mas agora, se fizermos uma manipulação algébrica na expressão fatorando os termos, obtemos:
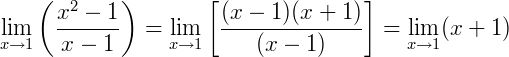
Como a expressão simplificada resultou em uma função 𝑔(𝑥) = 𝑥 + 1, que é contínua em 𝑥 = 1, podemos então calcular o seu limite:
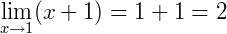
O limite de uma função 𝑓(𝑥) num ponto 𝑎 não depende do valor que 𝑓(𝑥) assume em 𝑎 mas sim, dos valores que 𝑓(𝑥) assume próximo de 𝑎 (ver artigo sobre limites). Esta manipulação algébrica, do exemplo acima, serviu apenas como uma forma de transformação da expressão, a fim de encontrarmos esses valores pois na sua forma original encontrávamos uma indeterminação.
Referências Bibliográficas:
GUIDORIZZI, Hamilton L. Um Curso de Cálculo: Volume 1. Rio de Janeiro: Editora LTC, 2001.
PISKUNOV, N. Cálculo Diferencial e Integral: Volume 1. Moscou: Editora Mir, 1977.
ROGAWSKI, Jon. Cálculo: Volume 1. Porto Alegre: Bookman, 2009.
Texto originalmente publicado em https://www.infoescola.com/matematica/limites-de-funcoes/