Limites no infinito

Limites no infinito (ou tendendo ao infinito) são aqueles em que a variável da função tende ao infinito. E representamos de duas formas:

$\displaystyle\lim_{x\rightarrow+\infty}f(x)=L$

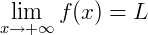
Para quando 𝑥 tende a “mais” infinito, ou:

$\displaystyle\lim_{x\rightarrow-\infty}f(x)=L$

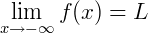
Quando 𝑥 tende a “menos” infinito.

Assim como a definição formal de limites, existe também uma definição formal para limites tendendo ao infinito, que não difere muito da de limites comuns. Abaixo, a definição para mais infinito:

Seja 𝑓 uma função e 𝑎 um ponto que pertence ao intervalo ]𝑎 ,+∞[, contido no domínio de 𝑓. Para qualquer 𝜀>0 existe 𝛿>0, com 𝛿>𝑎 tal que

𝑥 > 𝛿 ⇒ 𝐿−𝜀 < 𝑓(𝑥) < 𝐿+𝜀

O limite L, quando existe, é único e representamos por:

$\displaystyle\lim_{x\rightarrow+\infty}f(x)=L$

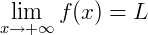
Há também uma definição para os limites tendendo a menos infinito:

Seja 𝑓 uma função e 𝑎 um ponto que pertence ao intervalo ]−∞ ,𝑎[, contido no domínio de 𝑓. Para qualquer 𝜀>0 existe 𝛿>0, com −𝛿<𝑎 tal que

𝑥 < −𝛿 ⇒ 𝐿−𝜀 < 𝑓(𝑥) < 𝐿+𝜀

O limite L, quando existe, é único e representamos por:

$\displaystyle\lim_{x\rightarrow-\infty}f(x)=L$

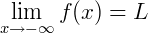
1) Vamos calcular um limite fundamental usando a definição formal de limites tendendo a mais infinito:

$\displaystyle\lim_{x\rightarrow+\infty}\frac{1}{x}=L$

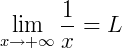
Primeiramente, analise o gráfico desta função:

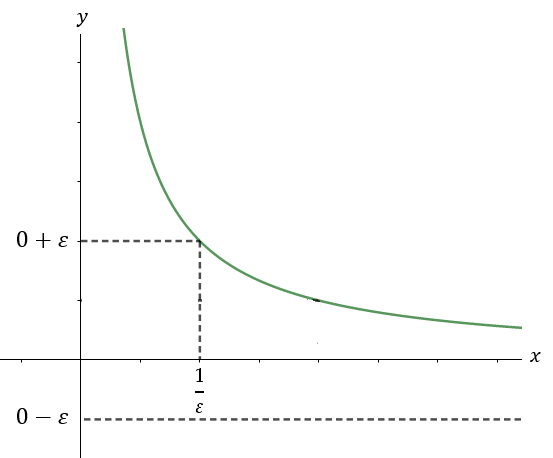
Observe que quanto maior for o valor de 𝑥, mais próximo 𝑓(𝑥) está de zero, o que intuitivamente poderíamos concluir que o limite desta função tendendo ao infinito é zero. Mas, podemos provar este fato usando a definição formal de limites:

Dado 𝜀>0 e, sendo 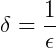$\delta=\frac{1}{\epsilon}$ dizemos que:

$x>\delta\Rightarrow 0<\frac{1}{x}<\epsilon$

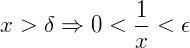
Logo,

$x>\delta\Rightarrow 0-\epsilon<\frac{1}{x}<0+\epsilon$

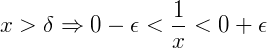
Concluindo então que:

$\displaystyle\lim_{x\rightarrow+\infty}\frac{1}{x}=0$

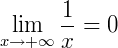
2) Agora, calculemos o limite:

$\displaystyle\lim_{x\rightarrow\pm\infty}\frac{\text{sen } x}{x}$

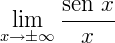
Construindo o seu gráfico temos:

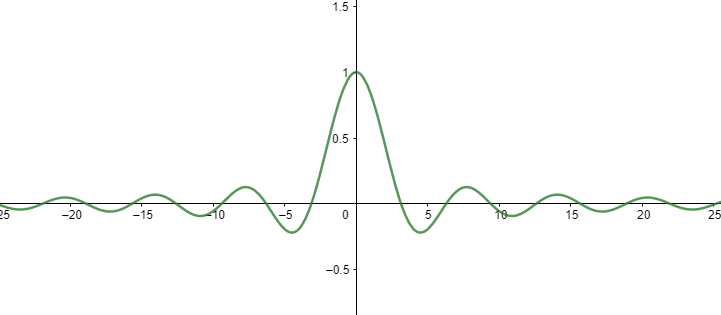
Apenas analisando o gráfico podemos dizer que:

$\displaystyle\lim_{x\rightarrow+\infty}\frac{\text{sen }x}{x}=\lim_{x\rightarrow-\infty}\frac{\text{sen }x}{x}=0$

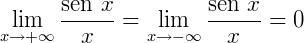
3) O limite a seguir terá um valor para mais infinito e outro para menos infinito:

$\displaystyle\lim_{x\rightarrow\infty}xe^x$

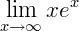
Observe o seu gráfico:

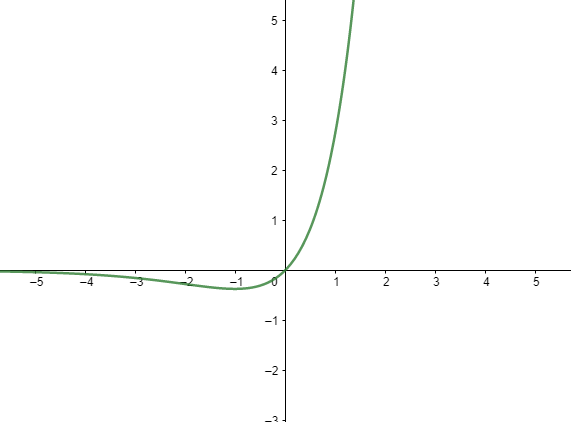
Analisando, percebemos que para −∞ o gráfico é uma assíntota do eixo 𝑥, o que remete a um limite igual a zero quanto maior for o valor de 𝑥. Mas, para +∞ o limite diverge para valores de 𝑥 cada vez maiores, o que nos dá um limite infinito, conclusão:

$\displaystyle\lim_{x\rightarrow+\infty}xe^x=+\infty$

$\displaystyle\lim_{x\rightarrow-\infty}xe^x=0$

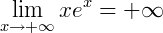
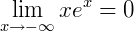
Referências Bibliográficas:

GUIDORIZZI, Hamilton L. Um Curso de Cálculo: Volume 1. Rio de Janeiro: Editora LTC, 2001.

PISKUNOV, N. Cálculo Diferencial e Integral: Volume 1. Moscou: Editora Mir, 1977.

ROGAWSKI, Jon. Cálculo: Volume 1. Porto Alegre: Bookman, 2009.

Texto originalmente publicado em https://www.infoescola.com/matematica/limites-no-infinito/