Para aqueles que estão habituados com matrizes e suas propriedades, veremos neste artigo algumas de suas aplicações no cotidiano como uma poderosa e eficaz ferramenta de trabalho para muitas áreas da ciência, tecnologia entre outros setores.
Conteúdo deste artigo
Teoria dos Grafos
A teoria dos grafos é basicamente o estudo das relações entre objetos de entre conjuntos. Estas relações são obtidas pelas estruturas chamadas de Grafos. A base para a teoria dos grafos são as matrizes e suas aplicações são diversas: Análise de influências entre pessoas, jogos de xadrez, distribuição de redes de água e esgoto para uma população e outros problemas famosos como o Problema do Caixeiro Viajante, que consiste em analisar uma forma otimizada o caminho que ele faria em uma viajem, começando num ponto e terminando a viajem nele, só que passando por todos os outros pontos apenas uma vez. A história da teoria dos grafos começa com Leonard Euler no famoso problema das pontes de Königsberg.

Computação Gráfica
Na computação gráfica, o uso de matrizes é evidente em muitas aplicações. Por exemplo, figuras tridimensionais num monitor de computador ou celulares só são possíveis graças a uma matriz que é gerada pelo processamento da imagem na tela. Consequentemente podemos fazer com que um objeto em 3 dimensões seja projetado no monitor e a álgebra de matrizes possibilita com que novas imagens possam ser geradas do mesmo objeto por meio da rotação, translação, alterando sua escala, etc. Pense nisso quando conseguimos dar um zoom numa imagem, e quando isto ocorre, alteramos a escala desta imagem e com isso o computador gerou uma matriz de coordenadas de imagem.
Tomografia Computadorizada
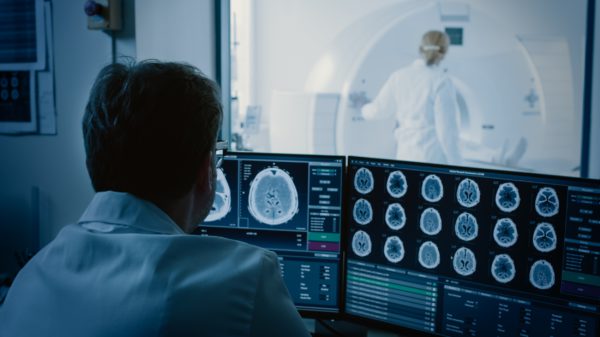
Ou exemplo computacional que envolve o uso de matrizes é na tomografia computadorizada. O intuito de um exame de tomografia é construir a imagem de um corte transversal de um corpo humano a partir da análise do escaneamento por raios X.
Criptografia
Outro exemplo do uso de matrizes é a criptografia, que é justamente o estudo de codificar ou decodificar mensagens a fim de torná-las secretas. Este método é muito antigo e desde os tempos de César, o imperador romano, já era utilizado. A famosa Cifra de César, ou cifra de substituição, é um tipo rudimentar de criptografia que consistia em substituir cada letra do alfabeto por alguma outra letra e reescrever a mensagem. Atualmente, o uso da criptografia evoluiu e consequentemente aumentou o interesse no assunto devido à necessidade de manter a privacidade da informação que nós acessamos. Sem ela, nossas senhas de redes sociais, dispositivos, contas bancárias entre outras seriam facilmente decifradas e não teríamos nenhuma segurança de nossas informações.
Existem ainda mais aplicações e ferramentas que utilizamos no dia a dia que dependem diretamente do uso de matrizes. Modelos econômicos preditivos, no desenvolvimento de jogos, na administração florestal, na internet com motores de busca mais eficientes e muito mais. Sem dúvida, suas aplicações são presentes em diversos ramos e profissões, logo vale a pena aprender esta disciplina sempre visando suas aplicações.
Referências bibliográficas:
ARFKEN, George B; WEBER, Hans J; HARRIS, Frank E. Física Matemática: Métodos Matemáticos para Engenharia e Física – 7ª Ed. Rio de Janeiro: Elsevier, 2017.
LIPSCHUTZ, Seymor; LIPSON, Marc. Álgebra Linear – 4ª Ed. Porto Alegre: Bookman, 2011.
ANTON, Howard; RORRES, Chris. Álgebra Linear – Com Aplicações – 10ª Ed. Porto Alegre: Bookman, 2012.
Texto originalmente publicado em https://www.infoescola.com/matematica/matrizes-no-cotidiano/