Duas circunferências, e , contidas em um mesmo plano, estão sujeitas a se relacionarem, de acordo com a posição que uma tem em relação a outra. Essas posições são estudadas de acordo com variações entre seus raios e a soma ou diferença entre eles.
Conteúdo deste artigo
Externas
Uma circunferência é externa a outra se os pontos de uma delas são exteriores à outra.
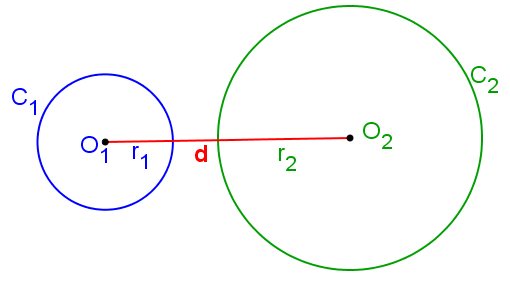
As circunferências C1(O1, r1) e C2(O2, r2) serão externas quando a distância entre seus centros for maior que a soma dos raios, ou seja: C1 e C2 são externas ⇔ d(O1, O2) > r1 + r2
Tangente externa
Duas circunferências são tangentes externas se elas têm um único ponto em comum e os demais pontos de uma são todos externos à outra.
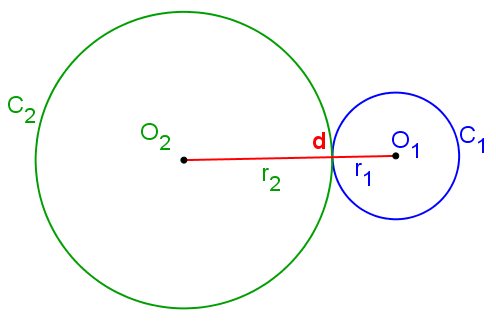
As circunferências C1(O1, r1) e C2(O2, r2) serão tangentes externas quando a distância entre seus centros for igual a soma dos raios, ou seja: C1 e C2 são externas ⇔ d(O1, O2) = r1 + r2
Tangente interna
Duas circunferências são tangentes internas se elas têm um único ponto em comum e os demais pontos de uma são todos interiores à outra.
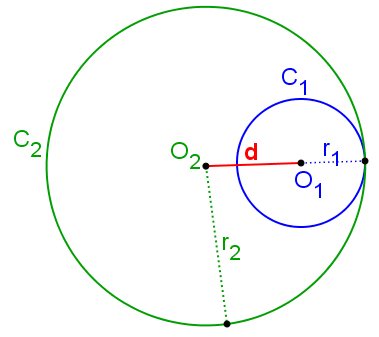
As circunferências C1(O1, r1) e C2(O2, r2) serão tangentes internas quando a distância entre seus centros for menor que a diferença entre os raios, ou seja: C1 e C2 são tangentes externas ⇔ d(O1, O2) = r1 - r2
Secantes
Duas circunferências são secantes se possuírem dois pontos distintos em comum.
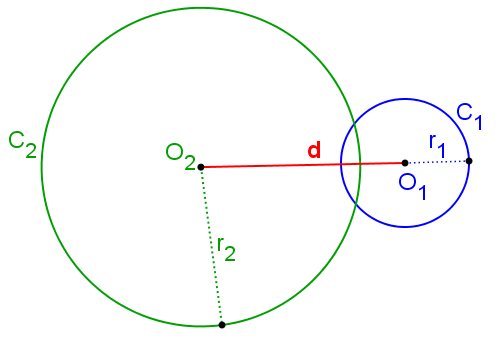
As circunferências C1(O1, r1) e C2(O2, r2) serão secantes quando a distância entre seus centros for menor que a soma dos raios e maior que a diferença entre os raios, ou seja: C1 e C2 são secantes ⇔ r1 - r2 < d(O1, O2) < r1 + r2
Observe que este caso está entre os casos de “Tangente externa” e “tangente interna”, por isso, a distância entre os centros estão entre essas duas condições.
Internas
Uma circunferência é interna a outra se os pontos de uma delas são interiores à outra.
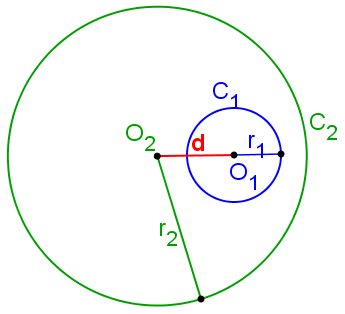
A circunferência C1(O1, r1) será interna a C2(O2, r2) quando a distância entre seus centros for menor que a diferença entre os raios de C1 e C2. C1 é interna a C2 ⇔ d(O1, O2) < r1 - r2
Concêntricas
Duas circunferências são concêntricas se seus centros são coincidentes. Nesse caso, uma circunferência sempre será interna a outra.
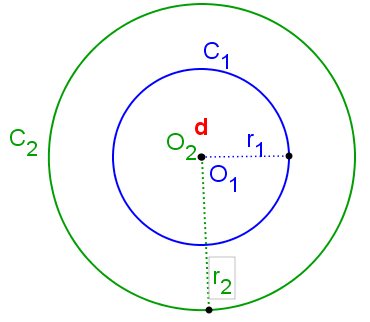
As circunferências C1(O1, r1) e C2(O2, r2) serão concêntricas quando a distância entre seus centros for zero. C1 e C2 são concêntricas ⇔ d(O1, O2) = 0
Coincidentes
Duas circunferências são coincidentes quando todos os pontos de uma são coincidentes à outra. Neste caso, obrigatoriamente elas serão também concêntricas.
Exemplo
1. Dê a posição de duas circunferências de raios r e R, sendo d a distância entre seus centros, nos casos abaixo.
- a) r = 2 cm; R = 5 cm; d = 10 cm.
- b) r = 6 cm; R = 8 cm; d = 10 cm.
Os casos envolvem somas e diferenças entre os raios, então:
a) A soma dos raios é igual a 7 e a diferença é igual a 3. A distância dos raios é maior que a soma entre eles. Por esse fato, as circunferências são externas.
b) A soma dos raios é igual a 14 e a diferença é igual a 2. A distância dos raios é menor que a soma entre eles e é maior que a diferença entre eles. Por esse fato, as circunferências são internas.
Referência:
DOLCE, Osvaldo; POMPEO, José Nicolau. Fundamentos de Matemática Elementar. Geometria Plana. Vol. 9. São Paulo: Atual, 1995.
Texto originalmente publicado em https://www.infoescola.com/matematica/posicoes-relativas-entre-duas-circunferencias/