O conceito de primitivas de funções é um precursor ao Teorema Fundamental do Cálculo e é aqui que a integração começa a fazer parte do estudo do cálculo. Então, apresentamos agora a definição:
“Seja 𝑓 uma função definida num intervalo real 𝐼 = [𝑎, 𝑏]. Uma primitiva (ou antiderivada) de 𝑓 em 𝐼 é uma função 𝐹 definida em 𝐼 onde F'(x)=f(x) para qualquer 𝑥 ∈ 𝐼".
Isto significa que seja uma função 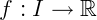 , e a função
, e a função 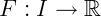 , então 𝐹 é primitiva de 𝑓 se a derivada de 𝐹 for igual a 𝑓. Dizemos também que neste caso, 𝑓é primitivável. Vamos agora apresentar algumas propriedades importantes:
, então 𝐹 é primitiva de 𝑓 se a derivada de 𝐹 for igual a 𝑓. Dizemos também que neste caso, 𝑓é primitivável. Vamos agora apresentar algumas propriedades importantes:
Dadas duas primitivas quaisquer, 𝐹1 e 𝐹2, de uma função 𝑓. A diferença entre duas primitivas é sempre uma constante.
Se a função 𝑓 é contínua em todo o espaço então ela também é primitivável. Esta definição dá origem ao Teorema Fundamental do Cálculo.
Podemos obter a família de primitivas de uma função, definida num intervalo 𝐼, calculando a seguinte integral:
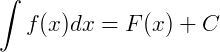
Sendo 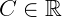 .
.
É importante lembrar que o uso da palavra “antiderivada”, que é a correspondente de “primitiva”, pode facilitar na memorização do conceito. Vejamos agora alguns exemplos:
1) Seja a função 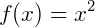 . A sua primitiva é dada por
. A sua primitiva é dada por 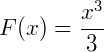 pois:
pois:
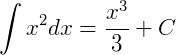
Logo:
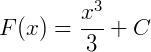
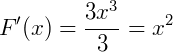
Note que perante este exemplo, chamarmos “primitivas” de “antiderivada” fica mais fácil para entender o conceito.
2) Para a função 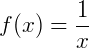 a sua antiderivada é
a sua antiderivada é 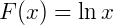 pois:
pois:
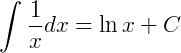
Portanto:
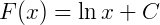
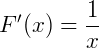
3) Agora, para 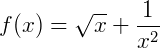 .
.
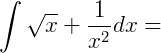
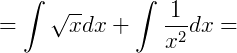
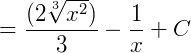
Logo:
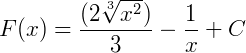
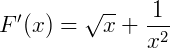
Referências Bibliográficas:
GUIDORIZZI, Hamilton L. Um Curso de Cálculo: Volume 1. Rio de Janeiro: Editora LTC, 2001.
PISKUNOV, N. Cálculo Diferencial e Integral: Volume 1. Moscou: Editora Mir, 1977.
ROGAWSKI, Jon. Cálculo: Volume 1. Porto Alegre: Bookman, 2009.
Texto originalmente publicado em https://www.infoescola.com/matematica/primitivas-de-funcoes/