Relações de Girard

As equações polinomiais são muito importantes e fazem parte de várias questões do nosso dia a dia, por exemplo, na física (lançamento de projéteis), na biologia (fotossíntese das plantas), no funcionamento de empresas (lucro de vendas, contabilidade, etc.), em serviços diários (ângulo antena parabólica), etc. Dessa forma, entender seu funcionamento e seus elementos se torna muito importante para resolver questões cotidianas.

Definição: Chama-se de equação polinomial de grau n, 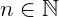$n\in\mathbb{N}$, na variável 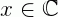$x\in\mathbb{C}$, toda equação que pode ser escrita da forma:

Onde a_n, a_n-1, ..., a₀ são os coeficientes reais do polinômio p(x), sendo que p(x) = a_nxⁿ + a_n-1x^n-1 + ... a₂x² + a₁x + a₀. Além disso, dizemos que 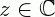$z\in\mathbb{C}$, é uma raiz de p(x) se p(z) = 0.

Muitos estudiosos trabalharam em diversos métodos para resolução desse tipo de equação e um deles foi Albert Girard. A ideia dele foi relacionar os coeficientes (reais ou complexos) e as raízes de uma equação polinomial. Essas relações ficaram conhecidas como Relações de Girard e são muito utilizadas até hoje. Vejamos como escrevê-las para polinômios de diversos graus.

Polinômios de 2° grau

Sejam 𝑝(𝑥)=𝑎𝑥²+𝑏𝑥+𝑐 , onde a ≠ 0, x₁ e x₂ raízes de p(x), então as relações de Girard são dadas por:

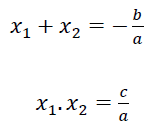
Essas são as famosas soma e produto das raízes de uma equação de segundo grau.

Polinômios de 3° grau

Considere o polinômio 𝑝(𝑥)=𝑎𝑥³+𝑏𝑥²+𝑐𝑥+𝑑, onde a ≠ 0, e sejam x₁, x₂ e x₃ raízes de p(x), então as relações de Girard são dadas por:

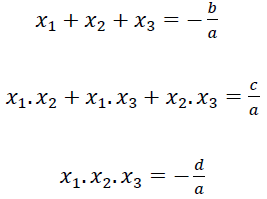
Polinômios de 4° grau

Seja o polinômio de quarto grau 𝑝(𝑥)=𝑎𝑥⁴+𝑏𝑥³+𝑐𝑥²+𝑑𝑥+𝑒, onde a ≠ 0, e sejam x₁, x₂, x₃ e x₄ raízes desse polinômio. Escrevemos que as relações de Girard de uma equação polinomial de quarto grau são:

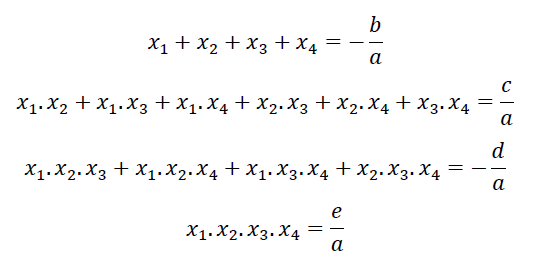
Polinômios de grau n

Se p(x)=𝑎_𝑛𝑥^𝑛+𝑎_𝑛−1𝑥^𝑛−1 + ⋯ + 𝑎₂𝑥² + 𝑎₁𝑥 + 𝑎₀ é um polinômio de grau n (n ≥ 1), onde a_n ≠ 0, cujas raízes são x₁, x₂,...,x_n, então temos que as relações de Girard podem ser escritas como:

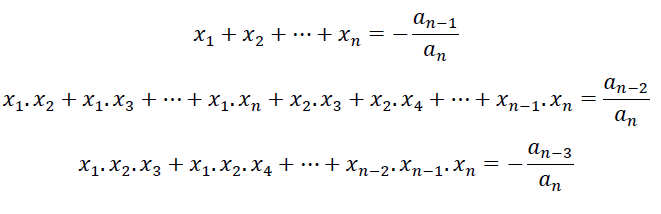
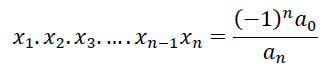
Ou seja, teremos tantas relações de Girard quanto for o grau do polinômio que compõe a equação polinomial estudada.

Exemplo:

(FUVEST-2004- adaptado) O produto de duas raízes do polinômio 𝑝(𝑥)=2𝑥³−7𝑥²+4𝑥+3 é igual a -1. Determine as raízes de p.

Solução:

Sejam r, s e t as raízes do polinômio p(x), do enunciado temos que r.s = -1 ↔ r = -1/s    (I)

Usando as relações de Girard e o resultado (I), e temos que:

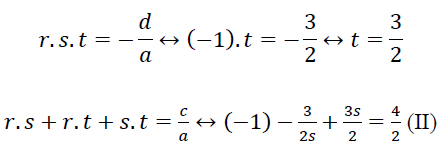Manipulando (II), encontramos que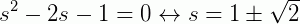 $s^2 -2s-1=0\leftrightarrow s=1\pm\sqrt{2}$

Logos as três raízes de p(x) são: 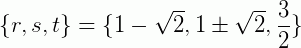$\{r, s, t\}=\{1-\sqrt{2}, 1\pm\sqrt{2},\frac{3}{2}\}$

Referências:

CASAROTO, Patrícia. Um estudo sobre equações polinomiais dedicado ao Ensino Básico. Tese (Mestrado em Matemática) – Universidade Estadual Paulista, Instituto de Geociências e Ciências Exatas. Rio Claro, SP. 2013.

Texto originalmente publicado em https://www.infoescola.com/matematica/relacoes-de-girard/