Soma de frações

Sabemos que frações são números representados na forma de uma razão entre de dois números inteiros. Somar frações não é uma tarefa difícil. Para isso vamos exemplificar primeiro uma soma de frações utilizando uma pizza.

Supondo que você e mais três amigos pediram uma pizza pelo telefone. Quando ela chegou você percebeu que ela não estava fatiada, como de costume. O problema surgiu quando você foi dividi-la entre os seus amigos. Como a pizza não estava fatiada, ficou mais difícil de definir o que seria um pedaço!

Vamos representar agora algumas formas de fatiar a pizza em pedaços de tamanhos diferentes:

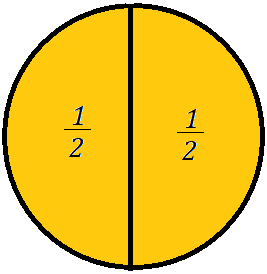
Soma das parcelas:

$\frac{1}{2}+\frac{1}{2} = \frac{2}{2} = 1$

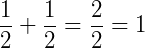
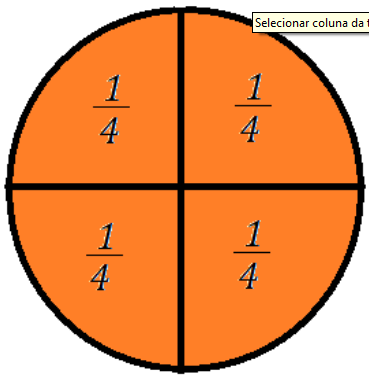
Soma das parcelas:

$\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4} = \frac{4}{4} = 1$

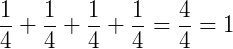
Porém, quase sempre quando compramos uma pizza, ela já vem cortada em 8 pedaços, o que em frações significa:

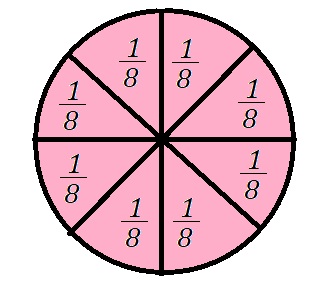
Soma das parcelas:

$\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8} = \frac{8}{8} = 1$

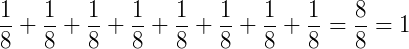
Soma de frações com denominadores iguais

A soma de frações com o mesmo denominador é obtida apenas somando os seus numeradores da seguinte maneira:

Exemplo 1) Veja a soma das frações abaixo:

$\frac{3}{7}+\frac{2}{7} = \frac{3+2}{7} = \frac{5}{7}$

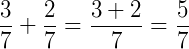
Exemplo 2) Agora a soma:

$\frac{1}{11}+\frac{5}{11}+\frac{3}{11} = \frac{1+5+3}{11}=\frac{9}{11}$

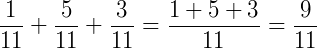
Soma de frações com denominadores diferentes

Podemos somar frações com diferentes denominadores de duas maneiras: Obtendo o MMC (mínimo múltiplo comum) dos denominadores ou multiplicando os denominadores, ou seja:

Exemplo 3) Vamos obter a soma da seguinte fração:

$\frac{1}{2}+\frac{3}{4}+\frac{5}{6}$

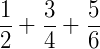
1º - MMC:

Obtendo o MMC de 2, 4 e 6 temos:

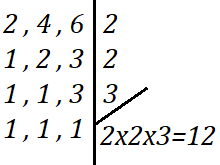
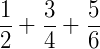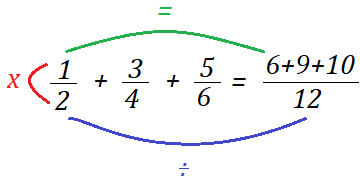
Sabemos então que 12 será o denominador do nosso resultado, agora devemos fazer as seguintes operações em relação a nossa soma de frações $\frac{1}{2}+\frac{3}{4}+\frac{5}{6}$.

Este passo significa que devemos dividir o numerador do resultado (aquele obtido pelo MMC) pelos numeradores das frações que estão somando e depois multiplicar pelos numeradores das mesmas. Observe que obtemos uma fração em que os numeradores estão em forma de soma e o denominador já é o próprio MMC obtido. Ou seja, a soma será dada por:

$\frac{1}{2}+\frac{3}{4}+\frac{5}{6} = \frac{6+9+10}{12} = \frac{25}{12}$

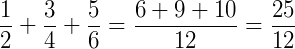
2º - Multiplicando os denominadores:

Utilizando a mesma soma como exemplo, procedemos da mesma maneira. Porém no lugar do MMC, colocamos o resultado da multiplicação dos denominadores, ou seja:

$\frac{1}{2}+\frac{3}{4}+\frac{5}{6} = \frac{24+36+40}{2 \cdot 4 \cdot 6} = \frac{100}{48}$

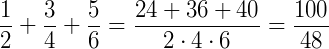
Simplificando a fração temos:

$\frac{100 \div 2}{48 \div 2} = \frac{50\div 2}{24 \div 2} = \frac{25}{12}$

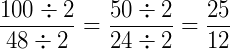
Referências Bibliográficas

DANTE, Luiz Roberto. Matemática: Contextos & Aplicações - Volume 1. São Paulo: Editora Ática, 2011.

Texto originalmente publicado em https://www.infoescola.com/matematica/soma-de-fracoes/