A resolução de sistemas lineares é um problema antigo, mas que ainda é muito útil, devido ao fato de muitos problemas computacionais se resumem a sistemas lineares gigantescos. Uma das maneiras de resolver um sistema linear é através do uso de determinantes (uma função matricial que associa uma matriz quadrada a um número real). A resolução de determinantes grandes pode ser realizada através de programas computacionais, porém, em alguns casos, queremos fazer isso manualmente. Quando isso acontece a ideia geral é realizar algum procedimento matemático que nos permita reduzir a ordem do determinante ou que nos permita simplificar esse determinante. Existem várias regras ou métodos para fazer isso, um deles é o chamado de teorema de Jacobi.
Definição: Seja uma matriz quadrada A, de ordem n (n ≥ 2). Se a uma fila (linha ou coluna) dessa matriz A, for adicionado uma múltipla de outra fila paralela a ela, obtemos uma matriz B, tal que: det(A) = det(B)
Ou seja, a ideia do Teorema de Jacobi é encontrar uma outra B, cujo determinante será o mesmo da matriz A.
A melhor forma de ver esse teorema na prática é através de exemplos.
Exemplos:
1) Seja a matriz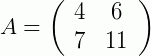 
, vamos encontrar o determinante utilizando o teorema de Jacobi.
Solução:
1°) escolha uma fila: Aqui escolho a 1° linha da matriz A:
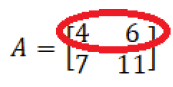
2°) Copie o termo da linha escolhida, multiplico os termos dessa linha (4 e 6) escolhida por algum valor (escolhi -2) e somar a linha seguinte (7 e 11):
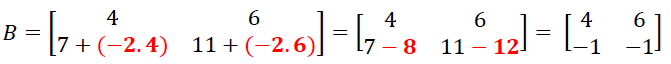
Agora, só para efeito de conferência, vamos encontrar os dois determinantes para confirmar a validade do teorema. Usando regra de Sarrus temos que: det(A) = 2 e det(B) = 2 . Logo o teorema vale.
2) Seja a matriz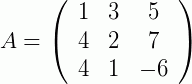 
. Vamos encontrar o determinante de A através do teorema de Jacobi.
Solução:
1°) Escolhendo uma fila: escolho a primeira coluna.
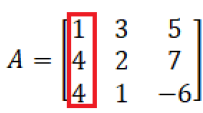
2°) Copio os termos da fila escolhida, multiplico eles por algum valor (aqui escolhemos -3) e somamos, termo a termo a uma das filas (aqui colunas) seguintes (copiando as restantes):
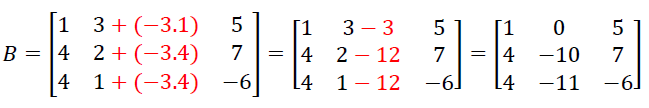
Novamente, vamos usar a Regra de Sarrus e encontrar o determinante das duas matrizes para ver que são iguais: det(A) = 117 e det(B) = 117.
Novamente o teorema é válido.
3) Seja a matriz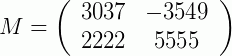 
, tal que det(M) = 24756413. Encontre o determinante da matriz 
.
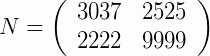Solução:
Podemos ver que as matrizes M e N tem a 1° coluna iguais, então podemos tentar fazer a segunda coluna da matriz N ser igual a 2° coluna da matriz M, e com isso, pelo teorema de Jacobi, elas terão o mesmo determinante.
Mantendo a primeira coluna, multiplicando ela pelo fator -2 e subtraindo da 2° coluna, temos uma nova matriz N’, idêntica a matriz M:
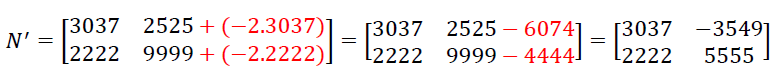
Logo, como N’=M, temos que det(N) = det(N') = det(M) = 24756413.
Observação:
A princípio esse teorema não parece ter grande utilidade, já que em muitos casos (como os dos exemplos 1 e 2) apenas trocamos os valores sem acrescentar ou facilitar nada, porém a grande sacada dele está justamente ai! Ao encontrarmos essa nova matriz, apenas com alguns valores trocados, podemos chegar a uma matriz conhecida ou até mesmo uma matriz mais simples de calcular o determinante (mesmo sem redução da ordem).
Texto originalmente publicado em https://www.infoescola.com/matematica/teorema-de-jacobi/