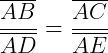Tales de Mileto foi um matemático e filósofo Grego do período pré-socrático que viveu em meados de 650 A.C. Tales, quando tentava determinar a altura de uma pirâmide, formulou um teorema que afirma:
“Se duas retas são transversais a um conjunto de três ou mais retas paralelas, então a razão entre os comprimentos de dois segmentos quaisquer determinados sobre uma delas é igual a razão entre os comprimentos dos segmentos correspondentes determinados sobre a outra.”
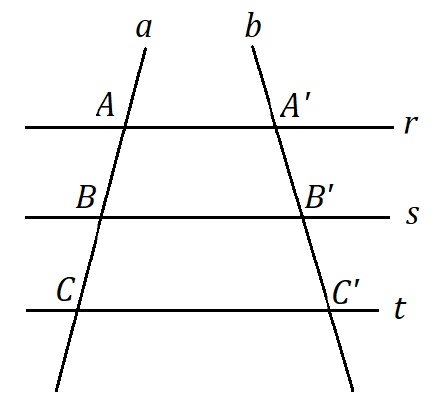
Para demonstrar o teorema de Tales devemos recorrer a definição do teorema fundamental da proporcionalidade, onde um feixe de paralelas determina, em duas transversais quaisquer, segmentos proporcionais. Assim, dados o feixe de paralelas r, s e t e as transversais a e b, temos:
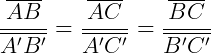
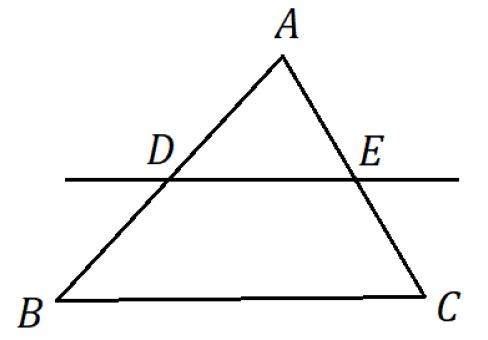
Num triangulo qualquer, se uma reta paralela a um dos lados deste triângulo corta os outros dois lados em pontos distintos, então ela os divide na mesma razão. Em outras palavras, seja um triângulo ABC, uma reta r paralela ao lado BC a qual intersecciona os lados AB e AC, respectivamente, nos pontos D e E, então:
Exemplo 1: Sejam as retas r, s e t tais que r // s // t. Vamos determinar a medida dos segmentos 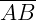 e
e 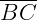 da figura abaixo:
da figura abaixo:
As medidas de cada segmento são:
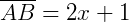
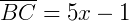
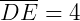
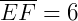
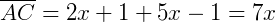
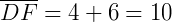
Pelo teorema de Tales, podemos então afirmar:
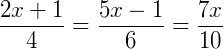
Para resolver esta equação podemos escolher dois entre os três termos acima na igualdade, por exemplo:
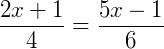
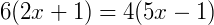
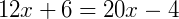
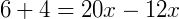
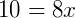
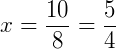
Então, as medidas valem 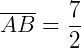 e
e 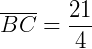 .
.
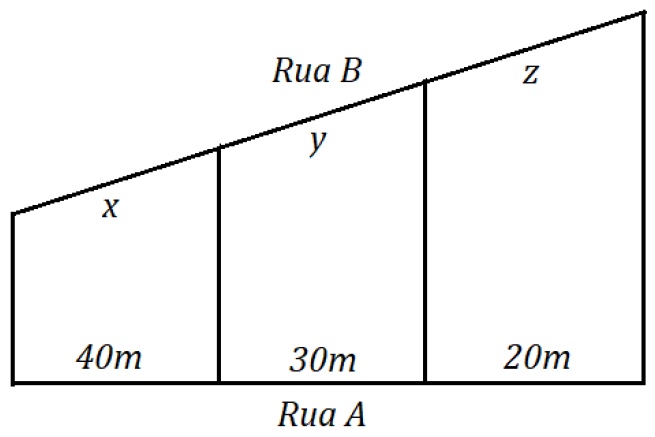
Exemplo 2: Agora, considere três terrenos que estão entre duas ruas, A e B. Sabendo que as medidas de cada terreno de frente a rua A são 40 m, 30 m e 20 m, vamos determinar a medida de cada terreno para a rua B sabendo que a frente para essa rua tem 180 m. Vamos ilustrar segundo o nosso problema um esboço dos terrenos:
Pelo enunciado podemos dizer que 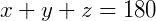 , então pelo teorema de Tales, a relação dos seus lados será dada por:
, então pelo teorema de Tales, a relação dos seus lados será dada por:
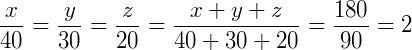
Assim como no exemplo anterior, precisamos determinar o valor de cada medida x, y e z da figura. No caso, todas as razões são iguais a 2. O que nos traz:
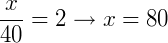
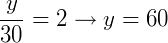
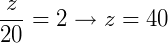
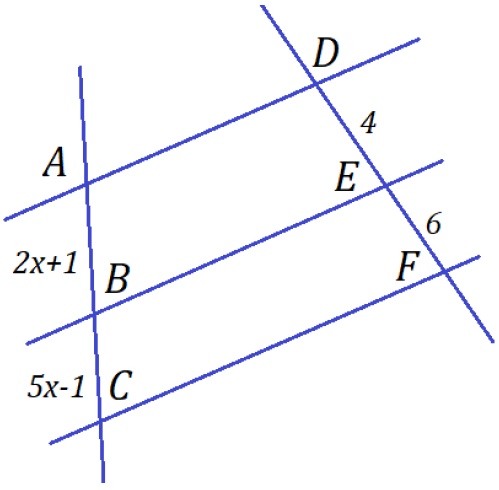
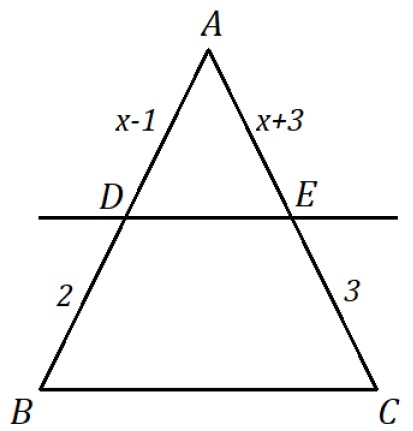
Exemplo 3: Agora, um exemplo com um triângulo onde os segmentos 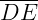 e
e 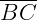 são paralelos. Vamos determinar o valor das medidas
são paralelos. Vamos determinar o valor das medidas 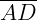 e
e 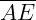 .
.
Pela definição do teorema podemos:
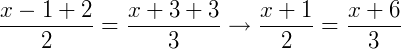
Desenvolvendo a expressão, temos:
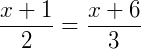
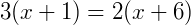
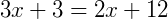
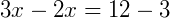
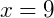
Então, as medidas são 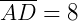 e
e 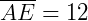 .
.
Teorema de Tales no círculo
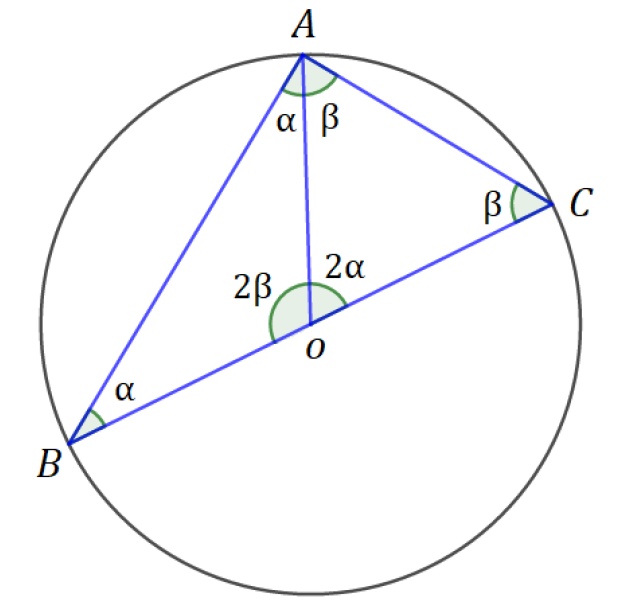
Existe ainda um caso especial do teorema de Tales a partir da definição do teorema do ângulo inscrito. Seja um triangulo qualquer ABC inscrito em uma circunferência, se a medida 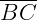 for o diâmetro desta circunferência, então os pontos A, B e C formam um triângulo retângulo. Veja a figura abaixo:
for o diâmetro desta circunferência, então os pontos A, B e C formam um triângulo retângulo. Veja a figura abaixo:
Pela figura temos as relações:
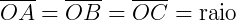
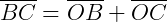
Logo, podemos dizer que os triângulos 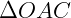 e
e 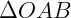 são isósceles e que:
são isósceles e que:
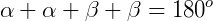
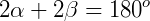
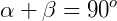
Concluindo então que o triângulo ABC é retângulo.
Referências Bibliográficas:
REZENDE, Eliane Q. F.; QUEIROZ, Maria L. B. Geometria Euclidiana Plana e Construções Geométricas. Campinas: Editora UNICAMP, 2000.
DANTE, Luiz Roberto. Matemática: Contextos & Aplicações - Volume 1. São Paulo: Editora Ática, 2011.
Texto originalmente publicado em https://www.infoescola.com/matematica/teorema-de-tales/