Trabalhando com Valores Percentuais Negativos - Matemática

Trabalhamos com porcentagem todos os dias e quase sempre sem perceber. Taxas de juros são dadas em porcentagem, descontos em lojas, ganhos de comissão em vendas são calculados sob uma porcentagem dos ganhos, sociedade de empresas é também dividida por uma porcentagem para cada sócio, entre inúmeros outros exemplos práticos.

A porcentagem é uma medida cuja base é igual a 100. Podemos expressar esta proporção entre dois inteiros como uma fração cujo denominador é igual a 100. Em outras palavras dizemos que dado um valor x:

$\frac{x}{100}=x\%$

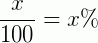
É possível, no nosso cotidiano, que exista a possibilidade em que precisamos trabalhar com valores percentuais negativos. Isso pode ocorrer quando estamos calculando variações percentuais de algumas quantidades. De um modo geral, a formula que determina a variação entre dois valores é dada por:

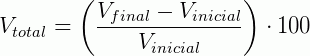
$V_{total}=\left(\frac{V_{final}-V_{inicial}}{V_{inicial}}\right)\cdot 100$

Exemplo 1) Um produto exposto numa vitrine está anunciado com a seguinte promoção:

De R$ 150,00

Por R$ 120,00

Para sabermos a variação percentual deste produto, usando a formula, temos:

$V_{total}=\left(\frac{V_{final}-V_{inicial}}{V_{inicial}}\right)\cdot 100$

$V_{total}=\left(\frac{120-150}{150}\right)\cdot 100$

$V_{total}=\left(\frac{-30}{150}\right)\cdot 100$

$V_{total}=(-0.2)\cdot 100$

$V_{total}=-20\%$

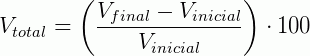
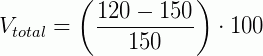
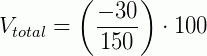
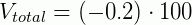
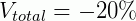
Isso significa que, o produto perdeu 20% do seu valor inicial, ou seja, teve uma variação de 20% a menos do seu valor.

Exemplo 2) No supermercado, uma lata de inseticida está escrito no rótulo:

Embalagem Econômica – Leve 395 ml e pague 300 ml

Sabemos então que existe um desconto, na lata promocional, de 95 ml do produto. Vamos calcular nesse caso o desconto percentual equivalente. Usando a formula, temos:

$V_{total}=\left(\frac{300-395}{395}\right)\cdot 100$

$V_{total}=\left(\frac{-95}{394}\right)\cdot 100$

$V_{total}=(-0.24)\cdot 100$

$V_{total}=-24\%$

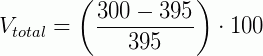
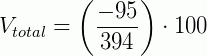
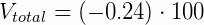
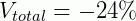
O que nos dá um desconto de 24% na embalagem econômica.

Exemplo 3) Um micro empresário que está conferindo o seu livro caixa tem no final de um mês os valores da sua receita e das suas despesas. Esses valores são:

Despesas – R$ 1950,35

Receitas – R$ 1235,87

Ele percebe que está no prejuízo, mas decidiu saber qual foi o valor em porcentagem que ele está no vermelho. Para sabermos, em porcentagem qual foi a variação percentual, usamos a formula:

$V_{total}=\left(\frac{1235,87-1950,35}{1950,35}\right)\cdot 100$

$V_{total}=\left(\frac{-714,48}{1950,35}\right)\cdot 100$

$V_{total}=(-0.3663)\cdot 100$

$V_{total}=-36,63\%$

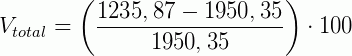
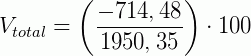
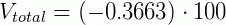
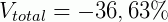
Referências bibliográficas:

DANTE, Luiz Roberto. Matemática: Contextos & Aplicações - Volume 1. São Paulo: Editora Ática, 2011.

Texto originalmente publicado em https://www.infoescola.com/matematica/trabalhando-com-valores-percentuais-negativos/