Volume da pirâmide

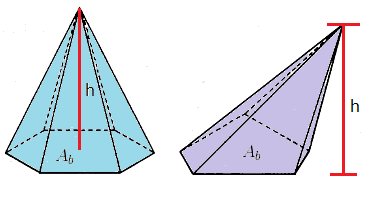
Dada uma pirâmide de área da base A_b e altura h. O seu volume (V) será: 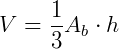$V = \frac{1}{3} A_b \cdot h$.

É muito difícil demonstrar essa fórmula, mas o que devemos perceber dela é a seguinte ideia: o volume da pirâmide é um terço do volume de um prisma com mesma base e altura.

Pirâmide de área da base e altura h.

Exemplo:

Pirâmide de base quadrada de lado 6 cm e altura 10 cm. Seu volume é de:

$V = \frac{1}{3} 6^2 \cdot 10$

$V = \frac{1}{3} 360$

$V = 120 cm^3$

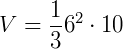
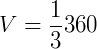
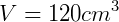
Pirâmide de base hexagonal de lado 4 cm e altura 5 cm. Sabendo que a fórmula de área de um hexágono é 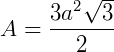$A = \frac{3a^2 \sqrt{3}}{2}$ (sendo "a" a medida de um lado do hexágono), seu volume é de:

$V = \frac{1}{3} \cdot \frac{3 \cdot 4^2 \sqrt{3}}{2} \cdot 5$

$V = \frac{1}{3} \cdot \frac{3 \cdot 16 \sqrt{3}}{2} \cdot 5$

$V = \frac{1}{3} \cdot \frac{48 \sqrt{3}}{2} \cdot 5$

$V = \frac{1}{3} \cdot 24 \sqrt{3} \cdot 5$

$V = \frac{1}{3} \cdot 120 \sqrt{3}$

$V = 40 \sqrt{3} \approx 69,28 cm^3$

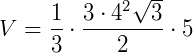
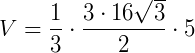
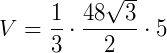
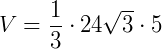
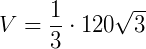
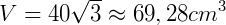
Texto originalmente publicado em https://www.infoescola.com/matematica/volume-da-piramide/