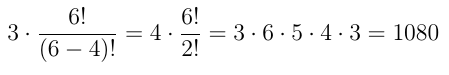Conteúdo deste artigo
Fatorial
Na resolução dos problemas de contagem é comum aparecerem produtos de fatores naturais sucessivos, tais como:
De quantas maneiras diferentes cinco pessoas podem ocupar cinco lugares em uma fila?
Resolução:
Aplicando o princípio fundamental da contagem (PFC), temos:
5 . 4 . 3 . 2 . 1 = 120 maneiras diferentes
Porém, se houvesse 30 pessoas para ocupar 30 lugares numa fila, teríamos que realizar o produto:
30 . 29. 28 . 27 . ... . 4 . 3. 2. 1
Para facilitar esse tipo de cálculo, utilizamos uma notação especial, o fatorial.
Definição de fatorial: dado um número natural n, definimos o fatorial de n (indicado por n!) por meio das relações:
- n! = n . (n-1).(n-2). ... . 3 . 2 . 1 para n ≥ 1
- Se n = 1, 1! = 1
- Se n = 0, 0! = 1
Note que o fatorial de n representa o produto dos n primeiros naturais positivos, escritos desde n até 1. Assim, temos, por exemplo:
3! = 3 . 2 . 1 = 6
5! = 5 . 4 . 3 . 2 . 1 = 120
Arranjo simples
O princípio multiplicativo é a ferramenta básica utilizada para resolver problemas de contagem. Sua aplicação direta na resolução de problemas pode às vezes tornar-se trabalhosa. Percebemos, contudo, que alguns problemas possuem características em comum e são recorrentes. Iremos a seguir, definir o agrupamento chamado Arranjo Simples.
O quê é um arranjo simples?
Suponha que com os dígitos 2, 3, 4, 5 e 6 você queira criar senhas de três algarismos distintos. Vamos enumerar algumas possibilidades:
- 235 e 352: Nesse caso, os dígitos são os mesmos, porém, estão em ordem diferente, o que faz com que as senhas obtidas sejam diferentes.
- 643 e 523: Nesse caso, as senhas formadas possuem dígitos diferentes, o que as torna distintas.
Cada um desses números é chamado de arranjo simples dos cinco elementos dados, tomados três a três.
Chamamos de arranjo simples de n elementos tomados p a p, em que n > p, a todo agrupamento de p elementos escolhidos entre os n elementos dados, que se diferenciam um do outro pela ordem em que aparecem no agrupamento ou por sua natureza.
Indica-se: 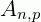 ou
ou 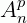 .
.
Cálculo do número de arranjo simples
Inicialmente, vamos resolver o seguinte problema:
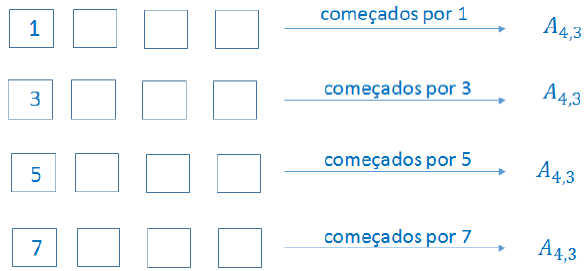
Com os algarismos: 2, 3, 4, 5 e 6, quantos números de três algarismos distintos podemos formar?
Resolução:
Formar um número de três algarismos distintos pode ser considerado um arranjo simples e a ação constituída de três etapas sucessivas, a saber:
- 1ª) escolha do algarismo das centenas: temos cinco possibilidades;
- 2ª) escolha do algarismo das dezenas: como não pode haver repetição de algarismo, devemos ter um algarismo diferente do algarismo escolhido para a centena. Assim, há quatro possibilidades;
- 3ª) escolha do algarismo das unidades: devemos ter um algarismo diferente dos dois anteriores (centena e dezena). Assim, há apenas três possibilidades.
Aplicando o princípio fundamental da contagem (PFC), temos: 5 x 4 x 3 = 60 números.
Logo,
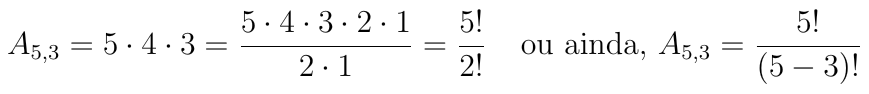
Generalizando, temos a fórmula de arranjo simples, tomados p a p, que indicamos por:
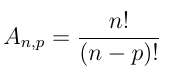
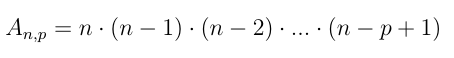
Exercícios resolvidos
1º) Em uma sala há 8 cadeiras enfileiradas e 4 pessoas. Calcule o número de modos distintos das pessoas ocuparem as cadeiras.
Resolução:
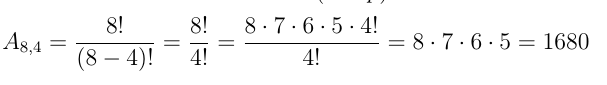
2º) Quantos números, entre 1000 e 8000, podemos formar com os algarismos ímpares, sem os repetir?
Resolução:
Os algarismos ímpares são: 1, 3, 5, 7 e 9
Como os números procurados têm quatro algarismos e estão compreendidos entre 1000 e 7000, temos:
Logo, o número total é de:
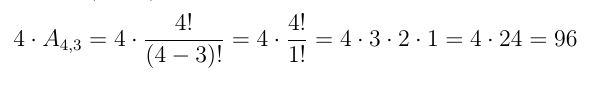
3º) Um automóvel comporta dois passageiros nos bancos da frente e três, no de trás. Calcule o número de alternativas distintas para o automóvel com pessoas escolhidas dentre sete, de modo que uma dessas pessoas nunca ocupe um lugar nos bancos da frente.
Resolução:
O número total de pessoas é igual a 7, logo:
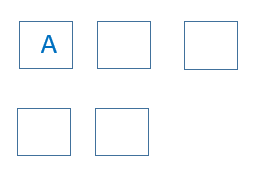
Fixando a pessoa A no banco de trás, restam 6 pessoas para ocuparem os quatro lugares restantes, isto é: 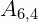
Como a pessoa A pode ser colocada em três lugares no banco de trás, temos:
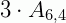
Logo:
4º) Considere a palavra MATRIZES. Quantos anagramas de 4 letras distintas podemos formar:
- a) começando com a letra T?
- b) terminando com as letras ZE?
- c) de modo que contenha a letra A?
Resolução:
Anagrama é uma espécie de jogo de palavras criado com a reorganização das letras de uma palavra para gerar outras palavras. Como a ordem das letras importa, temos arranjo simples.
a) O número total de letras da palavra MATRIZES é 8, então, começam pela letra T: 8 – 1 = 7 = n
Os arranjos eram tomados 4 a 4, mas, retirando a letra T (uma letra): 4 – 1 = 3 = p
Então:
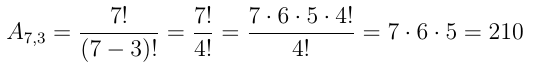
b) n = 8 – 2 (ZE) ⇒ n = 6 e p = 4 – 2 ⇒ p = 2
Então:
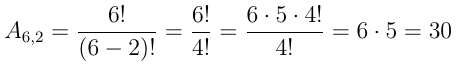
c) Vamos retirar a letra A e formar os agrupamentos com as 7 letras restantes, tomadas 3 a 3. Para cada um deles, existirão 4 maneiras de colocar a letra A.
Logo, teremos:
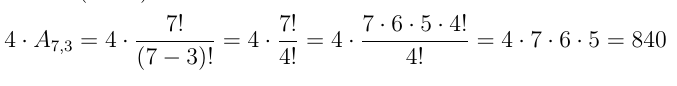
Leia também:
Referências bibliográficas:
1. MORGADO, Augusto C.; CARVALHO, João B. P. de; CARVALHO, Paulo Cezar P.; FERNANDEZ, Pedro – Análise Combinatória e Probabilidade – 9ª ed. – Rio de Janeiro, SBM, 1991
2. SANTOS, José Plínio O.; MELL, Margarida P.; MURARI, Idani T. C. – Introdução à Análise Combinatória – 4ª edição revista – Rio de Janeiro: Editora Ciência Moderna, 2007.
3. LIMA, Elon Lages. A Matemática do Ensino Médio. Volume 2, 6.ed. Coleção do Professor de Matemática. Rio de Janeiro: SBM, 2006
Texto originalmente publicado em https://www.infoescola.com/combinatoria/arranjo-simples/