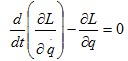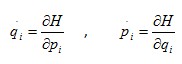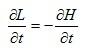A Física tenta explicar os fenômenos naturais a partir da análise de cada sistema isolado. Cada um destes sistemas obedece a um certo conjunto de leis que regem os fenômenos que mudam a configuração dos componentes do sistema com o tempo. Para alguns casos, é mais cômodo utilizar a Mecânica Newtoniana, utilizando um sistema de coordenadas cartesianas. Mas em geral os fenômenos requerem ferramentas poderosas, que consigam ter uma aplicação mais geral. Para isto se torna necessário escrever as equações do movimento para qualquer sistema utilizando as coordenadas generalizadas.
Cada partícula tem três coordenadas, no sistema cartesiano. Mas para n partículas, pode ser adotado um espaço denominado espaço das configurações, o qual tem 3n coordenadas. Deste modo, ao invés de n corpos com três coordenadas, o sistema tratará de um corpo com 3n coordenadas generalizadas. Por exemplo, um problema de 2 corpos e três eixos coordenados pode ser descrito como sendo o problema de um corpo com seis coordenadas generalizadas, dada por 3n, de modo que 3n = 3.2 = 6, onde n é o número de corpos e o fator 3 corresponde às três coordenadas do sistema cartesiano. (LEECH, J. W, segundo OLIVEIRA, 1971.)
Mas aparentemente seria mais difícil resolver um problema com seis coordenadas. Mas há artifícios para eliminar algumas delas, pois não serão necessárias para a resolução do problema. Isto porque há algumas restrições ao movimento livre do sistema, os chamados vínculos.
Dentre as formulações mais utilizadas pela Mecânica Clássica, destacam-se as formulações de Lagrange, Hamilton e Jacobi. Estes foram responsáveis pela criação de novas ferramentas para aplicar nos estudos dos fenômenos físicos em sistemas complexos. Tais ferramentas servem pra eliminar as dificuldades no cálculo vetorial de sistemas em movimento. Mas como isto seria possível? Bem, em primeiro lugar é necessário realizar uma transformação de coordenadas, transcrevendo o sistema utilizando coordenadas com todas as variáveis na forma escalar. Para isto, escreve-se o sistema em função da energia. Também é interessante eliminar variáveis indesejadas, escrevendo as equações de vínculo, que eliminam as chamadas forças de vínculo.
Ao eliminar os vínculos, reduz-se o número de graus de liberdade do sistema. Teremos S equações do movimento para qualquer sistema, de modo que S = 3.n – P, onde n é o número de corpos que compõe o sistema e P é o número de vínculos.
Um exemplo de equação de vínculo bastante conhecido é a equação do círculo, que limita o movimento de um objeto a uma distância constante de um ponto fixo, dada pelo raio da circunferência em questão. No caso da Máquina de Atwood, seria o comprimento de um conector inextensível que liga as duas massas. Para estas equações já pode-se eliminar uma variável em um dos eixos coordenados, pois o movimento pode ser restrito a um plano. Considerando o plano xy, teríamos para o objeto se movimentando no círculo:
x² + y² = R
z = 0
Isto implica em apenas uma equação de Lagrange para este problema, pois fazendo S = 3.n – P, teremos que S = 3.1 – 2, visto que temos duas equações de vínculo.
E para a máquina de Atwood, teríamos as seguintes restrições ao movimento livre do sistema:
z = 0
y1 + y2 = l
Ou seja, o comprimento do fio é dado pela soma das distâncias de cada massa ao ponto de apoio. Neste caso, também teremos apenas uma equação de Lagrange. Nota-se que nestes dois problemas temos vínculos holônomos e esclerônomos, pois podem serem escritos em forma de igualdade e são independentes do tempo.
Quando conveniente, transforma-se as coordenadas de cartesianas para sistema de coordenadas cilíndricas ou esféricas. Geralmente, usa-se as equações de transformação conhecidas. Exemplo: para o círculo, teremos um ângulo θ e um raio R. Como o sistema está restrito a um plano, poderemos escrever em coordenadas cilíndricas. Assim, teremos:
x = R.cosθ
y = R.senθ
z = 0
Na formulação Lagrangeana, basicamente se utiliza a energia cinética T e a energia potencial V envolvidas. A diferença entre a energia cinética é a equação de Lagrange conforme mostra a equação a seguir.
L = T – V
Segue para a resolução desta equação há de se satisfazer a seguinte propriedade:
No caso da formulação Hamiltoniana utiliza a energia total do sistema, dada pela equação a seguir.
H = T + V
Isto é válido para sistemas conservativos com o sistema de coordenadas independentes do tempo, ou seja, fixo no espaço.
Para se chegar às equações do movimento pela formulação de Hamilton satisfazerem as propriedades escritas a seguir, onde possivelmente surgirão coordenadas ignoráveis ou cíclicas.
Referências bibliográficas:
LEECH, J. W., BSc. PhD. Mecânica Analítica. Traduzido por OLIVEIRA, Carlos Campos de. Ed. Ao livro técnico S. A. e Editora da Universidade de São Paulo. Rio de Janeiro, 1971. 160p.
Texto originalmente publicado em https://www.infoescola.com/fisica/mecanica-classica/