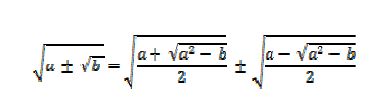Bháskara Acharya nasceu em 1.114 na Índia em uma família tradicional de astrólogos indianos. Com uma orientação científica dedicada à matemática e a astronomia tornou-se diretor ainda jovem no Observatório de Ujjain, o maior centro de pesquisas matemáticas e astronômicas da Índia. Seu tratado de álgebra foi base para a álgebra da Europa após alguns séculos. Escreveu o Siddhanta-siromani aos 36 anos em 1.150 sobre assuntos astronômicos e o Bijaganita sobre álgebra o que o fez se tornar o matemático mais famoso da época.
No Bijaganita Bhaskara propõe equações quadráticas e diz que as duas soluções que podem ser encontradas são igualmente aceitáveis. No Siddhantasiromani, que é sobre astronomia matemática, Bhaskara traz alguns resultados interessantes de trigonometria, entre eles estão:
sen (a + b) = sen a . sen b + cos a .sen b
e
sen (a – b) = sen a . cos b – cos a . sen b
(CELESTINO; PACHECO, 2006).
Não se pode dizer que Bháskara descobriu a fórmula de Bháskara, pois as fórmulas só vieram a surgir 400 anos após sua morte. O fato é que no Bijaganita o que consta sobre as equações determinadas de 2º grau é cópia de outros escritos matemáticos. Nas equações indeterminadas do 2º grau teve grande contribuição exposta no referido livro em relação a invenção do método do chakravala e a modificação do método Kuttaka.
Influências ao pensamento de Bháskara
Bháskara ao continuar a obra de Brahmagupta e descobrir a solução geral da equação de pell px² +1=y², onde ele resolveu para p = 8,11,32,61 e 67 e a solução de um problema de divisão por zero afirmando também que este quociente seria infinito. Bhaskara tinha conhecimento de que a equação x2=9 tinha duas soluções, apresentando a seguinte regra:
A matemática hindu exerce considerável influência em todo o mundo. Os hindus tinham conhecimento da raiz quadrada e cúbica, podendo citar como exemplo os algarismos. Esse povo influenciou bastante a álgebra onde os problemas aritméticos eram resolvidos por falsa posição ou pelo método de inversão. Um exemplo de solução por inversão consta no livro Lilavati de Bhaskara que diz:
Linda donzela de olhos resplandecentes, uma vez que entendeis o método de inversão correto, dizei-me qual é o número que multiplicado por 3, depois acrescido de ¾ do produto, depois dividido por 7, diminuído de 1/3 do quociente, multiplicado por si mesmo, diminuído de 52, pela extração da raiz quadrada, adição de 8 e divisão por 10 resulta no número 2?
Nesse caso o método de inversão inicia no número 2 e se opera para trás. Quando Bhaskara pede a adição de 8 significa redução de 8, e divisão de 10 significa multiplicação por 10.
Os hindus contribuíram para a matemática com a função do seno na trigonometria. (BROWN. EDU, 2009). Os indianos inventaram o zero. Ao estudar os livros de matemática da Índia, o matemático al-Khowarizmi escreveu um livro chamado “sobre a arte hindu de calcular” explicando como funcionava os dez símbolos hindus. (EDUCAR, 2009).
A fórmula de Bháskara é utilizada para determinar as raízes de uma equação de 2º grau. Ressalta-se que esta fórmula só recebe este nome no Brasil. Referências sobre a fórmula de Bháskara já havia sido encontrada em textos babilônicos há mais de 4.000 anos em tábuas cuneiformes. Na Grécia as equações de segundo grau eram resolvidas através de construções geométricas.
Referências:
BROWN.EDU. História da Matemática na Índia. Disponível em: http://www.brown.edu/
CELESTINO, Kamila Gonçalves; PACHECO, Edilson Roberto. Bháskara: algumas evidências. Disponível em: http://www.pucrs.br/edipucrs/
EDUCAR. História da Matemática. Disponível em: http://educar.sc.usp.br/
Texto originalmente publicado em https://www.infoescola.com/matematica/a-matematica-indiana-e-suas-contribuicoes/