Análise combinatória

A Análise combinatória é a parte da Matemática que estuda os problemas de contagem. Ela surgiu da necessidade de se calcular o número de possibilidades que podem ocorrer numa certa experiência, sem precisar descrever cada uma dessas possibilidades.

Alguns problemas bem simples podem ser resolvidos enumerando-se todas as possibilidades. Quando descrevemos todas as possibilidades de uma experiência ou evento, fazemos uma contagem direta.

No dia-a-dia, estamos acostumados a fazer contagens diretas como, por exemplo, quantos dias faltam para o início de nossas férias, de quantas maneiras diferentes podemos combinar 3 blusas com 2 calças diferentes, quantos são os resultados possíveis ao lançar uma moeda duas vezes seguidas, etc.

Em outras situações, entretanto, a enumeração torna-se muito trabalhosa ou, por vezes, impraticável.

Surge, então, a necessidade de utilizarmos algumas técnicas de contagem.

Diagrama de árvore

O diagrama de árvore ou diagrama das possibilidades é um esquema utilizado para enumerar todas as possibilidades de um evento com o objetivo de facilitar a resolução dos problemas de contagem.

Note que a árvore é construída da esquerda para a direita e que o número de “ramos” que saem de cada ponto corresponde ao número de possibilidades em que o evento pode ocorrer.

Por exemplo, retomemos o nosso problema de como combinar 2 calças e 3 blusas diferentes.

Pelo diagrama acima, temos:

Podemos concluir, portanto, que são 6 possibilidades.

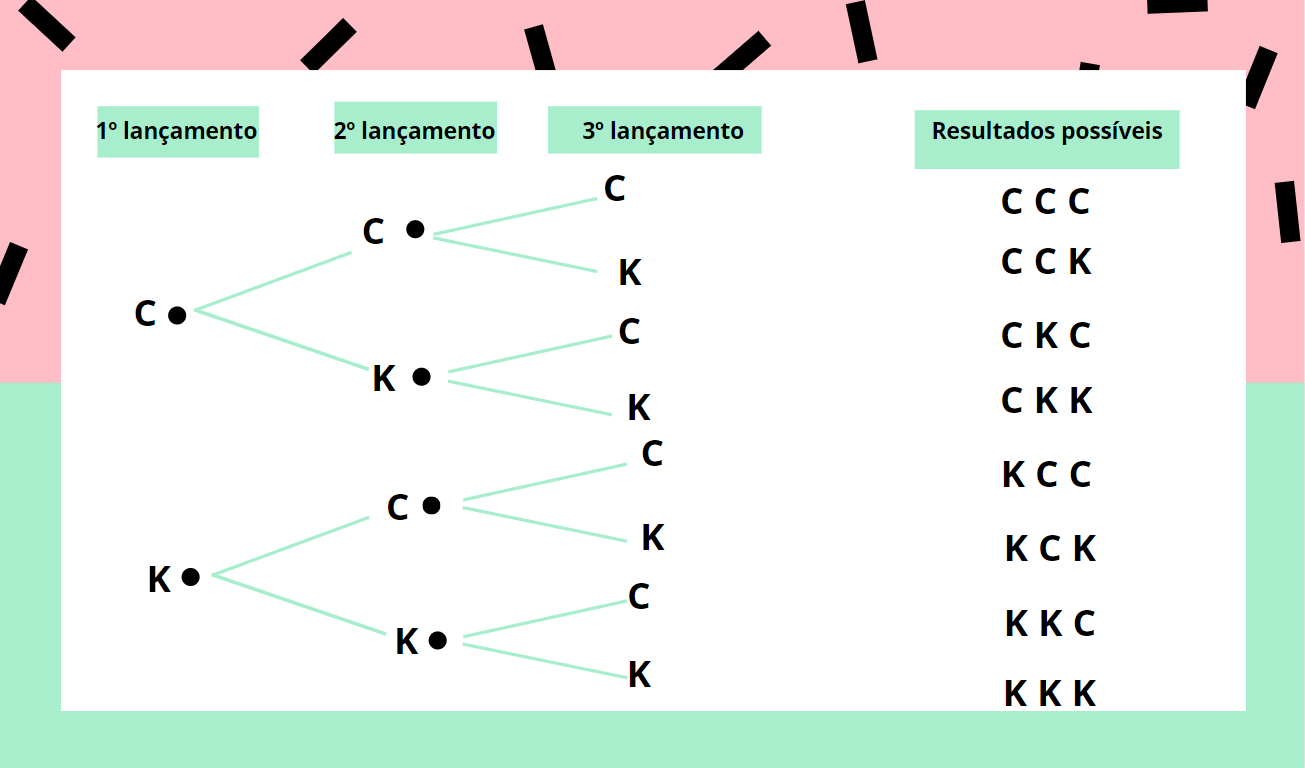
Uma moeda tem duas faces: cara (C) e coroa (K). Lança-se a moeda três vezes consecutivas e observa-se qual face ficou voltada para cima. Quais e quantos são os resultados possíveis.

Podemos notar, pelo diagrama de árvore, ao lado, que são os resultados possíveis são:

Ω = {(C, C, C); (C, C, K); (C, K, C); (C, K, K); (K, C, C); (K, C, K);(K, K, C); (K, K, K)}

Total de possibilidades: 8

Princípio Fundamental da Contagem (PFC)

Nos casos em que as alternativas de escolha forem muitas, o diagrama de árvore é pouco prático. Para essas situações, usamos o princípio fundamental da contagem ou princípio multiplicativo, que é um método algébrico para determinar o número total de possibilidades.

Este método consiste em multiplicar o número de possibilidades de cada etapa do experimento. Para entendermos melhor, observe o infográfico abaixo:

Exercícios resolvidos de Análise combinatória

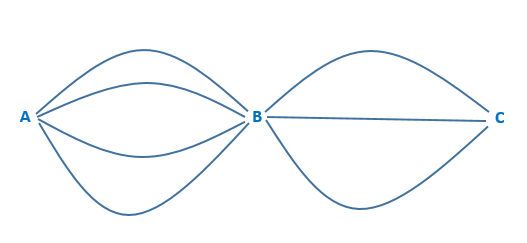
1º) Há quatro estradas ligando as cidades A e B, e três estradas ligando as cidades B e C. De quantas maneiras distintas pode-se ir de A até C, passando por B?

Resolução:

Aplicando o princípio fundamental da contagem (PFC), temos:

p₁: existem 4 possibilidades para ir da cidade A até a cidade B;

p₂: existem 3 possibilidades para ir da cidade B até a cidade C

Logo: existem p₁ . p₂ = 4 . 3 = 12 maneiras de ir de A até C, passando por B.

2º) Um teatro tem 4 portas. De quantas maneiras diferentes uma pessoa pode entrar e sair do teatro?

Resolução:

Aplicando o princípio fundamental da contagem (PFC), uma das principais ferramentas da Análise Combinatória, temos:

p₁: existem 5 possibilidades para entrar no teatro;

p₂: existem 5 possibilidades para sair do teatro.

Logo: existem p₁ . p₂ = 5 . 5 = 25 maneiras para entrar e sair do teatro.

3º) Quantos são os números de três algarismos distintos que podemos formar com os algarismos do sistema decimal?

Resolução:

Temos três posições para preencher: 1ª   2ª   3ª

Como não podemos começar com zero e os algarismos devem ser distintos, pelo (PFC), temos:

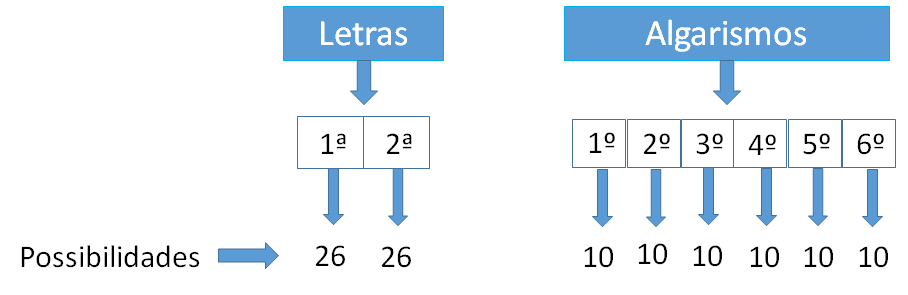
4º) Quantas placas de veículos podem ser criadas, se forem usadas duas letras de um alfabeto de 26 letras, seguidas por 4 algarismos?

Resolução:

Para formarmos uma placa de duas letras e 4 algarismos, passamos por 6 etapas. Sejam:

• k₁: número de possibilidades de escolher a primeira letra;
• k₂: número de possibilidades escolher a segunda letra;
• k₃: número de possibilidades escolher o primeiro algarismo;
• k₄: número de possibilidades escolher o segundo algarismo;
• k₅: número de possibilidades escolher o terceiro algarismo;
• k₆: número de possibilidades escolher o quarto algarismo.

Então, pelo princípio fundamental da contagem, temos:

k_{1 .} k_{2 .} k_{3 .} k_4. k_{5 .} k₆ = 26.26.10.10.10.10 = 6.760.000 possibilidades

Tipos de agrupamentos

Arranjo simples

Num conjunto A com n elementos, são arranjos simples todos os agrupamentos ordenados formados por p elementos distintos escolhidos entre os n elementos distintos dados, com p menor ou igual a n.

$A_{n, p}=\frac{n!}{(n-p)!}$

Arranjo com repetição

Chama-se arranjo com repetição ou arranjo completo, todo agrupamento de p elementos de um conjunto dado, com n elementos diferentes, onde a mudança de ordem determina grupos diferentes, podendo, porém, ter elementos repetidos.

$AR_{n,p}=n^p$

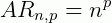
Permutação simples

A permutação é um arranjo de ordem máxima, ou seja, faz uso de todos os elementos do conjunto (n=p).

$P_n=p!$

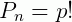
Permutação com repetição

Assim como na permutação simples, a diferença entre arranjo e permutação é que esta faz uso de todos os elementos do conjunto. Na permutação com repetição, as repetições são permitidas. Podemos estabelecer, entre o número de elementos n e as vezes que um mesmo elemento aparece, na fórmula.

Combinação simples

Chama-se combinação simples todo subconjunto formado por p elementos distintos de um conjunto de n elementos distintos dados. Neste tipo de agrupamento a ordem dos elementos não importa.

$C_{n,p}=\frac{n!}{((n-p)!)\cdot p!}$

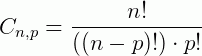
Referências bibliográficas:

1. MORGADO, Augusto C.; CARVALHO, João B. P. de; CARVALHO, Paulo Cezar P.; FERNANDEZ, Pedro – Análise Combinatória e Probabilidade – 9ª ed. – Rio de Janeiro, SBM, 1991

2. SANTOS, José Plínio O.; MELL, Margarida P.; MURARI, Idani T. C. – Introdução à Análise Combinatória – 4ª edição revista – Rio de Janeiro: Editora Ciência Moderna, 2007.

3. LIMA, Elon Lages. A Matemática do Ensino Médio. Volume 2, 6.ed. Coleção do Professor de Matemática. Rio de Janeiro: SBM, 2006

Texto originalmente publicado em https://www.infoescola.com/matematica/analise-combinatoria/