Arranjo com repetição - Matemática

O princípio multiplicativo é a ferramenta básica utilizada para resolver problemas de contagem. Sua aplicação direta na resolução de problemas pode às vezes tornar-se trabalhosa. Percebemos, contudo, que alguns problemas possuem características em comum e são recorrentes. Iremos a seguir, definir o agrupamento chamado Arranjo com repetição.

Conteúdo deste artigo

O que é um arranjo com repetição?
Cálculo do número de arranjos com repetição
Exercícios resolvidos

O que é um arranjo com repetição?

Arranjo com repetição, ou arranjo completo é um grupo de p elementos de um dado conjunto, com n elementos distintos, onde a mudança de ordem determina grupos diferentes podendo ter elementos repetidos.

Indica-se: AR_{n, p}

Cálculo do número de arranjos com repetição

No arranjo simples, pelo princípio fundamental da contagem, tínhamos:

$A_{n,p}=\frac{n!}{(n-p)!}$

$A_{n,p}=n\cdot(n-1)\cdot(n-2)\cdot\dots\cdot(n-p+1)$

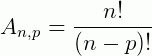
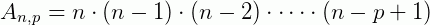
porque ele não admitia repetições. No arranjo com repetição, temos todos os elementos do conjunto à disposição a cada escolha, por isso, pelo princípio fundamental da contagem, temos:

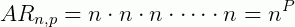
$AR_{n,p}=n\cdot n\cdot n\cdot\dots\cdot n=n^P$

(com P fatores)

Exercícios resolvidos

1º) Quantas placas de automóveis compostas de 2 letras nas duas primeiras posições, seguidas por quatro algarismos nas demais posições (sendo 26 letras do nosso alfabeto e sendo os algarismos do sistema decimal) podem ser formadas?

Resolução:

O número de pares de letras que poderão ser utilizadas é:

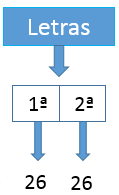
Pois não há condição de que sejam distintas e podem, portanto, se repetir. Assim, temos:

$AR_{26,2}=26^2=676$

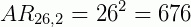
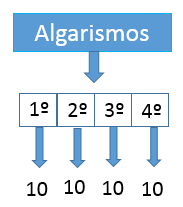
A quantidade de quádruplas de números que poderão ser utilizadas nas chapas que poderão ser feitas é:

$AR_{10,4}=10^4=10000$

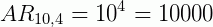
Resposta:

Então o total de chapas que poderão ser feitas é: 676 x 10000 = 6.760.000 placas

2º) Cinco sinaleiros estão alinhados. Cada um tem três bandeiras: uma amarela, uma verde e uma vermelha. Os cinco sinaleiros levantam uma bandeira cada, ao mesmo tempo, transmitindo-se assim um sinal. Quantos são os números de sinais diferentes que se pode transmitir?

Resolução:

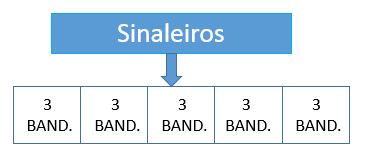
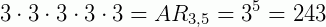
$3\cdot 3\cdot 3\cdot 3\cdot 3=AR_{3,5}=3^5=243$

3º) Um dia pode ter uma de 7 classificações: MB (muito bom), B (bom), R (regular), O (ótimo), P (péssimo), S (sofrível) e T (terrível). Os dias de uma semana são: domingo, segunda-feira, terça-feira, quarta-feira, quinta-feira, sexta-feira, sábado. Duas semanas se dizem distintas se dois dias de mesmo nome têm classificações distintas. Quantas semanas distintas, segundo o critério dado, existem?

Resolução:

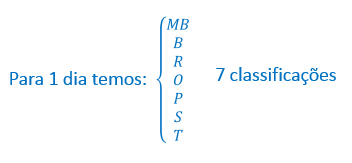
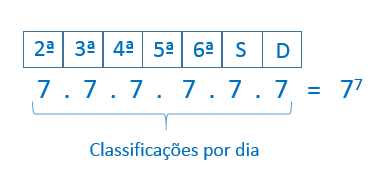
Usando a fórmula de arranjo com repetição, temos: AR_7,7 = 7⁷ = 823.543