Matriz Adjunta

No artigo sobre o Teorema de Laplace aprendemos uma forma generalizada para calcular o determinante de matrizes quadradas de qualquer ordem. Nele também nos é apresentado a definição de cofatores. Recordemos:

Considere uma matriz quadrada 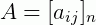$A=[a_{ij}]_n$ . O determinante desta matriz é igual a soma algébrica dos produtos dos elementos de uma linha i ou de uma coluna j pelos seus respectivos cofatores A_ij tais que:

$A_{ij}=(-1)^{i+j}|M_{ij}|$

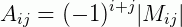
Onde M_ij é a submatriz de A, de ordem (n-1) que é obtida eliminando a i-ésima linha e a j-ésima coluna. O determinante de M_ij é chamado de menor do elemento a_ij de A e o cofator de a_ij é menor com “sinal”.

É chamada de matriz adjunta de A, ou simplesmente adj A, a transposta da matriz dos cofatores A_ij. Sendo assim podemos escrever:

adj A = (A_ij)^T

Vamos a um exemplo prático, seja uma matriz A dada por:

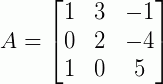
$A=\begin{bmatrix}1&3&-1\\0&2&-4\\1&0&5\end{bmatrix}$

Obtendo os menores:

$M_{11}=\begin{bmatrix}2&-4\\0&5\end{bmatrix}$	$M_{12}=\begin{bmatrix}0&-4\\1&5\end{bmatrix}$	$M_{13}=\begin{bmatrix}0&2\\1&0\end{bmatrix}$
$M_{21}=\begin{bmatrix}3&-1\\0&5\end{bmatrix}$	$M_{22}=\begin{bmatrix}1&-1\\1&5\end{bmatrix}$	$M_{23}=\begin{bmatrix}1&3\\1&0\end{bmatrix}$
$M_{31}=\begin{bmatrix}3&-1\\2&-4\end{bmatrix}$	$M_{32}=\begin{bmatrix}1&-1\\0&-4\end{bmatrix}$	$M_{33}=\begin{bmatrix}1&3\\0&2\end{bmatrix}$

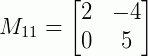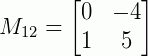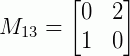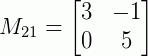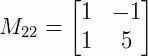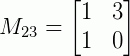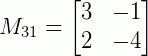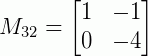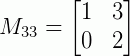Calculando então a sua matriz dos cofatores, termo por termo como na fórmula conhecida:

$A_{11}=(-1)^{1+1}|M_{11}|=10$

$A_{12}=(-1)^{1+2}|M_{12}|=-4$

$A_{13}=(-1)^{1+3}|M_{13}|=-2$

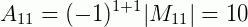
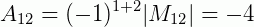
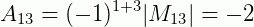
E assim por diante para todos os termos de A_ij:

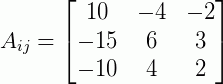
$A_{ij}=\begin{bmatrix}10&-4&-2\\-15&6&3\\-10&4&2\end{bmatrix}$

Onde podemos então concluir que a matriz adjunta será dada por:

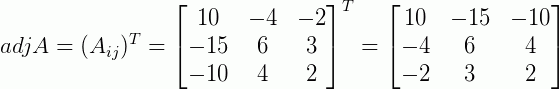
$adj A=(A_{ij})^T=\begin{bmatrix}10&-4&-2\\-15&6&3\\-10&4&2\end{bmatrix}^T=\begin{bmatrix}10&-15&-10\\-4&6&4\\-2&3&2\end{bmatrix}$

Teorema 1: Seja A uma matriz quadrada qualquer, então:

$A\cdot(adj A)=(adj A)\cdot A=|A|\cdot I$

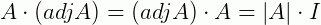
Onde I é a matriz identidade.

Teorema 2: Se 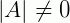$|A|\neq 0$ , então vale a igualdade:

$A^{-1}=\frac{1}{|A|}(adj A)$

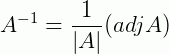
Onde A^-1 é a matriz inversa de A.

Referências bibliográficas:

ARFKEN, George B; WEBER, Hans J; HARRIS, Frank E. Física Matemática: Métodos Matemáticos para Engenharia e Física – 7ª Ed. Rio de Janeiro: Elsevier, 2017.

LIPSCHUTZ, Seymor; LIPSON, Marc. Álgebra Linear – 4ª Ed. Porto Alegre: Bookman, 2011.

Texto originalmente publicado em https://www.infoescola.com/matematica/matriz-adjunta/