Assim como somar ou subtrair matrizes, é possível também multiplicar matrizes. Se você ainda não leu os artigos sobre Matrizes, então leia! Será muito importante para entender melhor este conceito.
Conteúdo deste artigo
Condição Necessária
Antes de multiplicarmos matrizes, é preciso verificar se as mesmas podem ser multiplicadas mediante algumas definições. Então, para que seja possível a multiplicação entre matrizes, suponha que sejam duas, A e B, o número de colunas da matriz A deverá ser igual ao número de linhas da matriz BN. Um exemplo genérico:
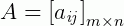
e
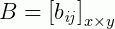
Note que na matriz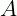 
, o número de linhas e de colunas são dados por 
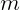e 
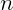, respectivamente. Na 
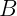, linhas e colunas são dados por 
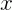e 
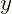, respectivamente. Agora, como citado acima, a multiplicação entr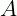e e 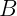só será possível se:
Ou seja, o número de colunas de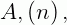 
é igual ao número de linhas de 
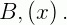Consequentemente, o resultado desta multiplicação nos dará uma matriz que terá a dimensão que será igual ao número de linhas de 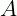e o número de colunas de 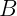. Vamos explicar de forma geral: Suponha que a multiplicação de 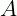por 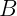resulte numa matriz que chamaremos de 
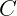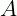. Se e 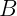cumprem o requisito , então:
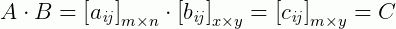
Agora vamos a um exemplo mais simples. Seja:
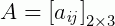
e
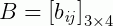
Como, o número de colunas de A é igual ao de linhas de B, então é possível a multiplicação, resultando na matriz C:
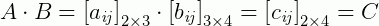
Vale reforçar que se esta condição não for satisfeita, não é possível multiplicar duas matrizes de nenhuma maneira.
Como Multiplicar Matrizes – Um Caso Simples
Vamos começar com um caso mais simples. Sejam duas matrizes A e B onde, A é uma matriz linha e B uma matriz coluna, ou seja:
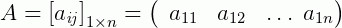
E claro, suponha que a condição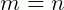 
é satisfeita neste caso (só assim será possível multiplicá-las). O produto delas resultará num escalar C onde 
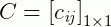. A multiplicação será dada por:
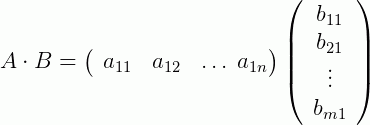
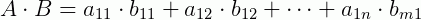
Exemplos:
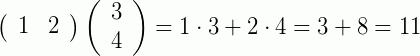
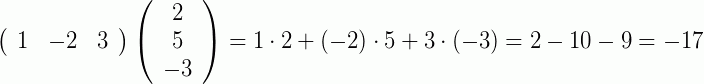
Perceba que, multiplicamos cada elemento da linha de A com o seu respectivo elemento da coluna de B.
Caso Geral da Multiplicação de Matrizes
Vamos com calma agora e apresentar o caso geral da multiplicação de matrizes de um modo formal e logo em seguida exemplos práticos:
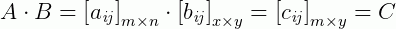
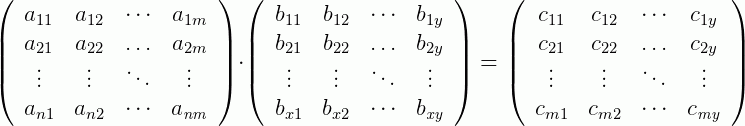
Onde cada ij-ésima entrada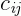 
, da matriz C resultante, é obtida pelo produto das i-ésimas entradas de A e as j-ésimas entradas de B, em outras palavras:
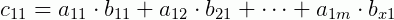
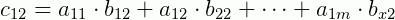
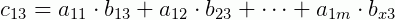
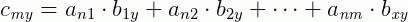
O que isto significa? Que fizemos nada mais é do que multiplicar cada linha de A com cada coluna de B e posicionamos este resultado na matriz C , de um modo bem similar com que fizemos no caso simples de matrizes linha e coluna quando multiplicadas. Vejamos:
Depois:
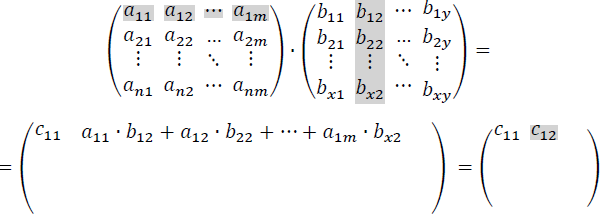
Continuando este procedimento para todas as linhas de A e todas as colunas de B , obtemos o produto das duas matrizes. Agora vamos aos exemplos práticos:
Exemplo 1: Sejam as matrizes A e B abaixo,
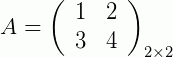e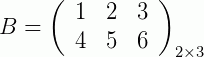 
, então 
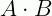será:
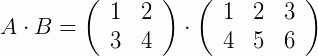
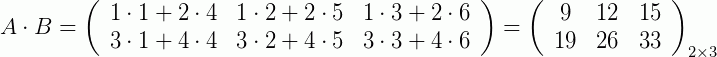
Exemplo 2: Para duas matrizes quadradas de ordem 2,
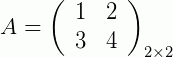e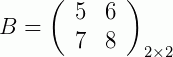 
, temos:
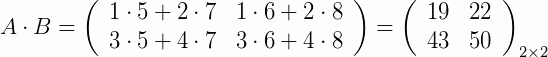
Exemplo 3: Agora, matrizes de ordem 3:
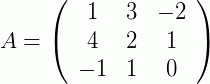e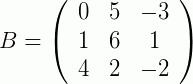 
;
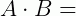
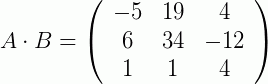
Propriedades Importantes
Dados A , B e C matrizes que podem ser multiplicadas entre si, então valem as propriedades:
1 –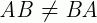 
, não há comutatividade na multiplicação de matrizes.
2 –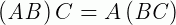 
3 –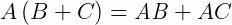 
4 –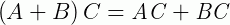 
5 –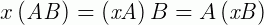 
, onde 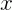é um escalar.
6 –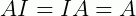 
, onde 
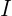é a matriz Identidade.
7 –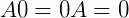 
, onde é a matriz nula.
Referências bibliográficas:
ARFKEN, George B; WEBER, Hans J; HARRIS, Frank E. Física Matemática: Métodos Matemáticos para Engenharia e Física – 7ª Ed. Rio de Janeiro: Elsevier, 2017.
LIPSCHUTZ, Seymor; LIPSON, Marc. Álgebra Linear – 4ª Ed. Porto Alegre: Bookman, 2011.
Texto originalmente publicado em https://www.infoescola.com/matematica/multiplicacao-de-matrizes/