O conjunto dos números naturais (ou o conjunto dos inteiros não negativos), representado pelo símbolo 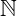 , é a nossa principal ferramenta de contagem. Eles são basicamente “os números que usamos para contar”: 2 carros, 12 ovos, 3 pessoas...
, é a nossa principal ferramenta de contagem. Eles são basicamente “os números que usamos para contar”: 2 carros, 12 ovos, 3 pessoas...
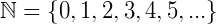
O homem primitivo precisava de uma representação simbólica para contabilizar seus elementos, objetos e tudo o que lhes pertenciam ou tinham a necessidade de administrar. Neste caso, o número zero ainda não era descrito como numeral, afinal, demorou milhares de anos até que por volta de 450 d.C., os hindus introduziram uma coluna vazia em seus ábacos donde veio o conceito de uma representação do vazio numericamente.
O zero é também um elemento de contagem, por isso ele faz parte dos números naturais. Porém em matemática podemos trabalhar com os números naturais sem o zero, onde simbolicamente representamos por:
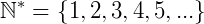
ou também por:

Uma definição formal da estrutura do conjunto dos naturais foi dada pelo matemático Giuseppe Peano, onde introduziu os famosos axiomas de Peano. Estes axiomas exibem os números naturais como ordinais, ou seja, objetos que ocupam lugares determinados em uma sequência. O número 1 é o primeiro natural, o 2 é o que sucede o 1, o 3 vem em seguida do 2, e assim por diante. Os números naturais também ocorrem como resultado de uma operação de contagem, então, o conjunto 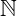 é infinito. Antes de enunciar estes axiomas vamos apresentar algumas propriedades a respeito dos números naturais. Comecemos pela adição:
é infinito. Antes de enunciar estes axiomas vamos apresentar algumas propriedades a respeito dos números naturais. Comecemos pela adição:
Para quaisquer 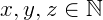 valem as propriedades:
valem as propriedades:
Associativa: 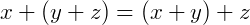
Comutativa: 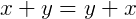
Lei do Corte: 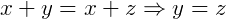
Elemento Neutro: 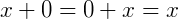
Agora, para a multiplicação:
Associativa: 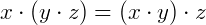
Comutativa: 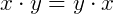
Lei do Corte: 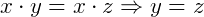
Monotonicidade: 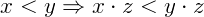
Estas propriedades foram construídas a partir dos axiomas de Peano onde, para melhor compreensão dos mesmos, recomenda-se um conhecimento básico sobre conjuntos numéricos e de funções. As definições abaixo consideram o conjunto dos naturais sem o zero (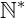 ). Enunciamos:
). Enunciamos:
Seja uma função 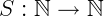 e para qualquer
e para qualquer 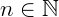 a lei de associação S(n), que é o valor em que a função S assume no ponto n, é chamada de sucessor de n.
a lei de associação S(n), que é o valor em que a função S assume no ponto n, é chamada de sucessor de n.
1º Axioma:
A função é injetiva 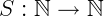 , ou seja, para todo
, ou seja, para todo 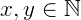 :
:
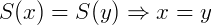
Isto significa que se dois números que pertencem aos naturais têm o mesmo sucessor então eles são iguais.
2º Axioma:
O conjunto 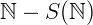 possui apenas um elemento. Em outras palavras, existe um único número natural que não é sucessor de nenhum outro, logo, este número é o um.
possui apenas um elemento. Em outras palavras, existe um único número natural que não é sucessor de nenhum outro, logo, este número é o um.
3º Axioma (Princípio da Indução):
Seja o subconjunto 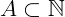 tal que
tal que 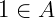 e, para qualquer
e, para qualquer 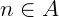 , temos que
, temos que 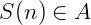 , então
, então 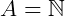 .
.
Estes axiomas servem para a construção dos números naturais, bem como todas as propriedades que derivam deles. Esta abordagem rigorosa serviu para estruturar o conceito de número que depois formaram a base para outros conjuntos numéricos usuais na matemática: os inteiros 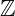 , os racionais
, os racionais 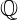 , os reais
, os reais 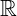 , etc.
, etc.
Referências Bibliográficas
MILIES, César Polcino; COELHO, Sônia Pitta. Números: Uma Introdução à Matemática. São Paulo: EDUSP,2013.
LIMA, Elon Lages. Curso de Análise: Volume 1. Rio de Janeiro: IMPA, 2017.
LIPSCHUTZ, Seymor; LIPSON, Marc. Matemática Discreta. Porto Alegre: Bookman, 2004
Texto originalmente publicado em https://www.infoescola.com/matematica/numeros-naturais/