Chamamos número racional todo número obtido da divisão (razão) entre dois inteiros, com o divisor não nulo.
Todo número racional pode ser escrito na forma de número inteiro, decimal exato ou dízima periódica.
Exemplos:
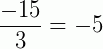
(inteiro)
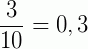
(decimal exato)
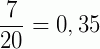
(decimal exato)
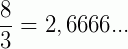
(dízima periódica)
Podemos definir o conjunto Q dos números racionais da seguinte forma:
Q = {x | 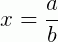 , com
, com 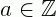 ,
, 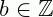 e
e 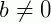 }
}
A forma 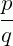 para se representar um número racional é denominada fração. O inteiro p é o numerador e o inteiro q≠0 é o denominador da fração.
para se representar um número racional é denominada fração. O inteiro p é o numerador e o inteiro q≠0 é o denominador da fração.
Conteúdo deste artigo
- Leitura de uma fração
- Fração própria, imprópria e aparente
- Número misto
- Transformação de número misto em fração imprópria
- Transformação de uma fração imprópria em número misto
- Simplificação de frações
- Comparações de frações
- Operações com números racionais
- Adição e subtração
- Multiplicação de números racionais (frações)
- Divisão de números racionais (frações)
Leitura de uma fração
Lê-se primeiramente o numerador e em seguida a unidade fracionária: meio, terço, quarto, etc.
Exemplos:

oito terços

dois quintos
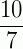
dez sétimos
Se o denominador é uma potência de 10, isto é, 10, 100, 1000, ... , lê-se o numerador acompanhado das palavras décimos, centésimos, milésimos, etc.
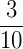
três décimos

onze centésimos
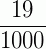
dezenove milésimos
Fração própria, imprópria e aparente
Fração própria: é aquela cujo numerador é menor que o denominador, isto é, a fração é menor que a unidade.
Exemplos: 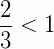 ,
, 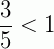
Fração imprópria: é aquela cujo numerador é maior que o denominador, isto é, a fração é maior ou igual a 1.
Exemplos: 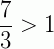 ,
, 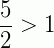 ,
, 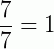
Fração aparente: é a fração em que o numerador é múltiplo do denominador.
Exemplos: 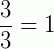 ,
, 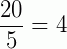 ,
, 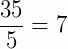
Número misto
A soma de um número natural com uma fração própria chama-se número misto, que em geral é representado sem sinal “mais” (+) colocado entre o número natural (ou inteiro) e a fração.
Exemplo:
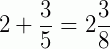
(lê-se: dois inteiros e três oitavos)
Transformação de número misto em fração imprópria
Multiplica-se a parte natural pelo denominador e ao produto soma-se o numerador, obtendo-se assim o numerador da fração procurada; o denominador é conservado o mesmo.
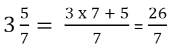
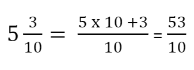
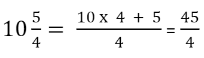
Transformação de uma fração imprópria em número misto
Divide-se o numerador pelo denominador. O quociente é a parte natural, o resto da divisão é o numerador, permanecendo para a fração própria o mesmo denominador.
Transformar uma fração imprópria em número misto é o mesmo que “extrair os inteiros” de uma fração imprópria.
Exemplos:
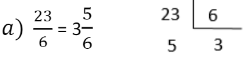
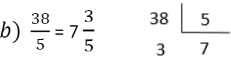
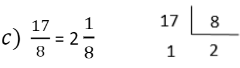
Frações equivalentes
Duas ou mais frações que representam a mesma porção da unidade são denominados frações equivalentes.
Exemplo:

Simplificação de frações
Simplificar uma fração é obter outra que lhe seja equivalente e de termos respectivamente menores.
Para simplificar uma fração basta dividir ambos os seus termos por um mesmo número diferente de zero.
Quando a fração não pode mais ser simplificada, diz-se que ela é irredutível. Neste caso, os termos da fração são primos entre si, isto é, não admitem divisores comuns além do número 1.
Exemplos:
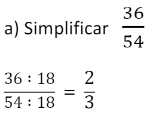
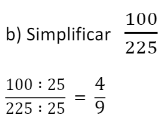
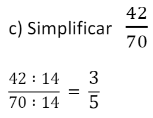
Comparações de frações
1º caso: Frações com o mesmo denominador
A maior é a que tem maior numerador
Exemplos:


2º caso: Frações com o mesmo numerador
A maior é a que tem menor denominador


3º caso: Frações com numeradores e denominadores diferentes
Basta reduzi-las ao mesmo denominador comum, por meio do mínimo múltiplo comum.
Exemplos:
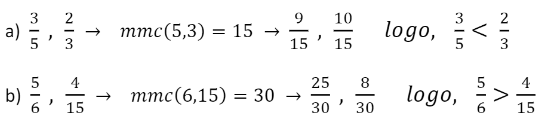
Operações com números racionais
Adição e subtração
1º caso: As frações têm o mesmo denominador
Neste caso, conserva-se o denominador e somam-se ou subtraem-se os numeradores.
Exemplos:
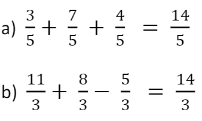
2º caso: As frações têm denominadores diferentes
Neste caso, reduzem-se as frações ao mesmo denominador e depois conserva-se o denominador e somam-se ou subtraem-se os numeradores.
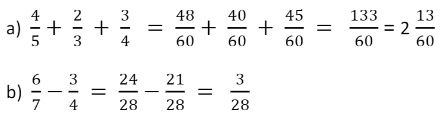
Multiplicação de números racionais (frações)
Multiplicam-se os numeradores entre si e os denominadores entre si.
Exemplos:
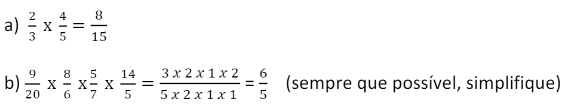
Divisão de números racionais (frações)
Para dividir duas frações, devemos multiplicar a primeira pelo inverso da segunda.
Exemplos:
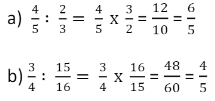
Texto originalmente publicado em https://www.infoescola.com/matematica/numeros-racionais/