Duas ou mais frações que representam a mesma porção da unidade são denominadas frações equivalentes.
Exemplo: 
, 
, 
, 
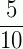, ... são todas equivalentes à fração 
.
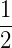Observação: O conjunto das frações equivalentes a uma fração dada chama-se classe de equivalência dessa fração.
Conteúdo deste artigo
Propriedades das frações
Fundamental: Pode-se multiplicar (ou dividir) os termos de um número fracionário por um número qualquer, diferente de zero, que se obtém sempre um representante da mesma classe de equivalência.
Do numerador: Quando se multiplica o numerador por um número, a fração fica multiplicada por esse número, e, quando se divide o numerador por um número diferente de zero, a fração fica dividida por esse número.
Exemplo: multiplicando 
por 2, obtemos a fração 
que é duas vezes a fração (dobro).
Do denominador: Quando se multiplica o denominador por um número diferente de zero, a fração fica dividida por esse número, e, quando se divide o denominador por um número diferente de zero, a fração fica multiplicada por esse número.
Exemplo: seja a fração 
. Multiplicando o seu denominador por 2, teremos 
que é duas vezes menor que ; a fração ficou dividida por 2.
Simplificação
Simplificar uma fração é obter outra que lhe seja equivalente e com termos respectivamente menores.
Para simplificar uma fração basta dividir ambos os termos por um mesmo número diferente de zero.
Quando a fração não pode mais ser simplificada, diz-se que ela é irredutível. Neste caso, os termos da fração são primos entre si, isto é, não admitem divisores comuns.
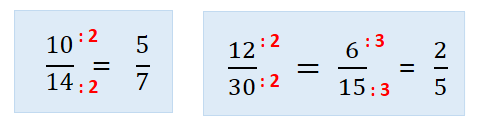
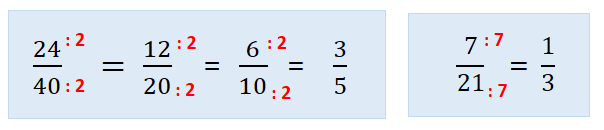
Processo prático para determinar frações equivalentes
1º exemplo: Vamos procurar uma fração equivalente a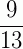 
cujo denominador seja 507.
2º exemplo: Vamos procurar uma fração equivalente a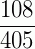 
cujo numerador seja 4.
Leia também:
Texto originalmente publicado em https://www.infoescola.com/matematica/fracoes-equivalentes/