Frações próprias são aquelas em que o numerador é menor que o denominador.
Por exemplo, são frações próprias:
![]()
Frações impróprias são aquelas em que o numerador é maior que o denominador.
Por exemplo, são frações impróprias:
![]()
Frações aparentes são aquelas em que o numerador é múltiplo do denominador.
Por exemplo, são frações aparentes:
![]()
Note que todas as frações aparentes citadas são também frações impróprias. Frações aparentes são formas de representar números inteiros.
![]()
Leia mais: Frações próprias, impróprias e aparentes.
Conteúdo deste artigo
Número Misto
A soma de um número natural com uma fração própria chama-se número misto, que em geral é representado sem sinal “mais” (+) colocado entre o número natural (ou inteiro) e a fração.
Exemplos:
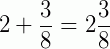
(lê-se: 2 inteiros e três oitavos)
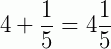
(lê-se: 4 inteiros e um quinto)
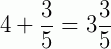
(lê-se: 4 inteiros e três quintos)
Transformação de uma fração imprópria em um número misto
1. Divide-se o numerador pelo denominador. O quociente é a parte natural, o resto da divisão é o numerador, permanecendo para a fração própria o mesmo denominador.
2. Transformar uma fração imprópria em um número misto é o mesmo que “extrair os inteiros” de uma fração imprópria.
Exemplo: Vamos transformar a fração 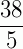 em um número misto.
em um número misto.
Na prática, dividimos o numerador pelo denominador.
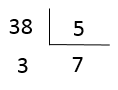
O quociente (7) corresponde à parte inteira, pois 5 cabe 7 “vezes inteiras” no 38. O resto (3) deve ser dividido em 5 partes iguais, ou seja, 3 : 5, o que pode ser representado pela fração  .
.
Então, podemos escrever: 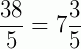
Veja como identificar nesse procedimento os termos do número expresso na forma mista:
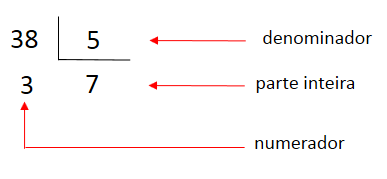
Transformação de um número misto em fração imprópria
Multiplica-se a parte natural pelo denominador e ao produto soma-se o numerador, obtendo-se assim o numerador da fração procurada; o denominador é conservado o mesmo.
a) Transformar 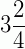 em fração imprópria.
em fração imprópria.
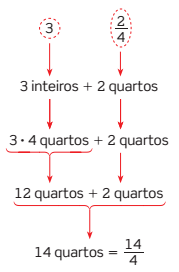
Assim, 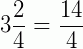 .
.
b) Transformar 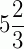 em fração imprópria.
em fração imprópria.
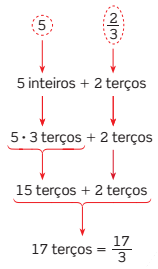
Assim, 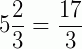 .
.
Leia também:
- Frações
- Frações equivalentes
- Soma de frações
- Subtração de frações
- Multiplicação de frações
- Divisão de frações
Texto originalmente publicado em https://www.infoescola.com/matematica/tipos-de-fracoes/