Quando falamos em potência, devemos lembrar que um número a que está elevado a uma potência n, significa que o número a deverá ser multiplicado n vezes, ou seja:

Sendo assim, quando queremos elevar uma fração a uma determinada potência devemos fazer o seguinte:
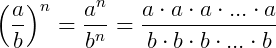
Existem ainda alguns exemplos importantes que envolvem potências e frações que valem a pena ser revistos:
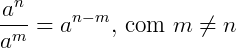 |
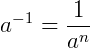 |
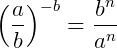 |
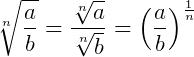 |
Exemplo 1)
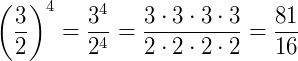
Exemplo 2)
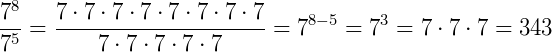
Exemplo 3)
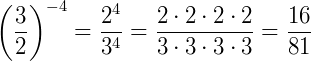
Exemplo 4)
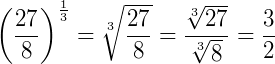
Exemplo 5)
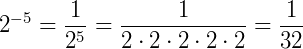
Leia também:
Referência:
DANTE, Luiz Roberto. Matemática: Contextos & Aplicações - Volume 1. São Paulo: Editora Ática, 2011.
Texto originalmente publicado em https://www.infoescola.com/matematica/potenciacao-de-fracoes/