Potenciação

A potenciação (ou exponenciação) é uma das operações básicas no universo dos números naturais onde um dado número é multiplicado por ele mesmo, uma quantidade n de vezes. Lembrando que para representar a soma de várias parcelas iguais, usamos a multiplicação, podemos recorrer à potenciação para expressar o produto de vários fatores iguais.

$a^n = b$

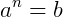
Onde:

• a = base;
• n = expoente;
• b = potência.

Assim, a base sempre será o valor do fator; o expoente é a quantidade de vezes que o fator repete; a potência é o resultado do produto.

Exemplo: 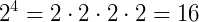$2^4 = 2 \cdot 2 \cdot 2 \cdot 2 = 16$

Uma potência a de grau n é o produto de n fatores iguais a a. Em outras palavras, dizemos que a está elevado à enésima potência.

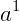$a^1$: dizemos que a está elevado à primeira potência.

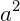$a^2$: dizemos que a está elevado à segunda potência. Potências com expoente igual a 2 são conhecidas como “quadrado”.

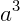$a^3$: dizemos que a está elevado à terceira potência. Potências com expoente igual a 3 são conhecidas como “cubo”.

Definições

Todo número elevado à zero é igual a um

$a^0 = 1$

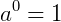
Potência com expoente 1

Qualquer número, elevado a 1 será igual a ele mesmo

$a^1 = a$

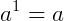
Toda potência de base 1 é igual ao próprio 1

Nas potências com base 1, dados por 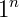$1^n$, sendo n pertencente aos reais, não importa o valor de "n", será sempre 1.

$1^n = 1$

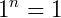
Potências com base igual a 0

Toda potência com base igual a 0 , 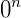$0^n$, sendo o expoente n >0, será igual a zero.

$0^n = 0$

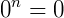
Propriedades da Potenciação

Multiplicação de potências de mesma base

Quando se multiplica potências de mesma base, têm-se uma nova potência onde a base é igual a base das parcelas e o expoente é a soma dos expoentes das parcelas.

$a^m \cdot a^n = a^{m+n}$

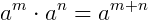
Em uma multiplicação de potências com a mesma base, conservamos a base e somamos os expoentes.

Exemplo: 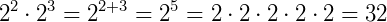$2^2 \cdot 2^3 = 2^{2+3} = 2^5 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 = 32$

Divisão de potências de mesma base

Quando se divide potências de mesma base, têm-se uma nova potência onde a base é igual a base do divisor e dividendo e o expoente é a diferença dos expoentes do divisor e dividendo.

$\frac{a^m}{a^n} = a^{m-n}$, $a \neq 0$

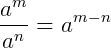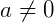
Em uma divisão de potências com a mesma base, conservamos a base e subtraímos os expoentes.

Exemplo: 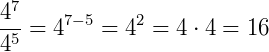$\frac{4^7}{4^5} = 4^{7-5} = 4^2 = 4 \cdot 4 = 16$

Potência com expoente negativo

Nas potências com expoente negativo, devemos inverter a base e inverter o sinal do expoente:

$a^{-m} = \left(\frac{1}{a}\right)^m$, $a \neq 0$

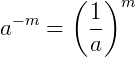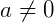
Exemplo: 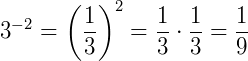$3^{-2} = \left(\frac{1}{3}\right)^2 = \frac{1}{3} \cdot \frac{1}{3} = \frac{1}{9}$

Potência de uma multiplicação

A multiplicação de dois ou mais fatores elevados a um dado expoente é igual a multiplicação desses fatores, cada um elevado ao mesmo expoente:

$(a \cdot b \cdot c)^n = a^n\cdot b^n \cdot c^n$

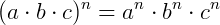
Exemplo: 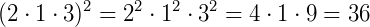$(2 \cdot 1 \cdot 3)^2 = 2^2 \cdot 1^2 \cdot 3^2= 4 \cdot 1 \cdot 9 = 36$

Potência de uma divisão

A divisão de dois fatores elevados a um dado expoente é igual a divisão desses fatores, cada um elevado ao mesmo expoente.

$\left(\frac{a}{b}\right)^n = \frac{a^n}{b^n}$, $b \neq 0$

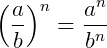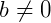
Exemplo: 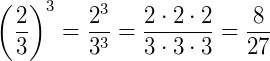$\left(\frac{2}{3}\right)^3 = \frac{2^3}{3^3} = \frac{2 \cdot 2 \cdot 2}{3 \cdot 3 \cdot 3} = \frac{8}{27}$

Potência de uma potência

A potência n da potência m de um número a é igual à potência de a cujo expoente é o produto dos expoentes m e n, ou seja:

$(a^n)^m = a^{n \cdot m}$

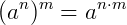
Exemplo: 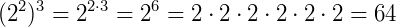$(2^2)^3 = 2^{2 \cdot 3} = 2^6 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 = 64$

Potência com expoente fracionário

Quando encontramos uma potência com expoente fracionário, devemos transformá-la em um radical, ou seja, em uma raiz, onde o numerador e o denominador do expoente serão respectivamente o índice e o expoente do radicando, assim:

$a^{\frac{m}{n}} = \sqrt[n]{a^m}$, $n \neq 0$

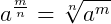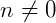
Exemplo: 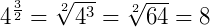$4^{\frac{3}{2}} = \sqrt[2]{4^3} = \sqrt[2]{64} = 8$

Potência de uma Raiz

Quando a base é composta de uma raiz, o expoente da potenciação passa a ser o expoente do radicando:

$(\sqrt[n]{a})^m = \sqrt[n]{a^m}$

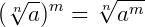
Exemplo: 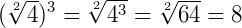$(\sqrt[2]{4})^3 = \sqrt[2]{4^3} = \sqrt[2]{64} = 8$

Potência com base negativa

Observe os exemplos abaixo:

$(-3)^2 = 9$

$-3^2= -9$

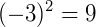
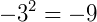
O sinal de negativo (-) na frente do 3 só fará parte da potenciação quando estiver dentro de um parêntese, caso contrário, ele continua no seu lugar no resultado.

Porém, no primeiro exemplo, o expoente é 2, número par, por isso o resultado final é positivo. Se fosse um número ímpar, o resultado seria negativo:

(-3)³ =

(-3) . (-3) . (-3) =

9 . (-3) = -27

se tirarmos os parênteses

-3³ =

- 3 . 3 . 3 =

-9 . 3 = -27

Leia também:

• Potenciação com números negativos
• Potenciação no dia a dia

Referências:

GIOVANNI, José Ruy; CASTRUCCI, Ângela (org.). Por trás da porta, que a matemática acontece. Campinas: UNICAMP, 2001.

IMENES, Luiz; LELLIS, Marcelo. Matemática. 5a a 8a série. Scipione, 1998.

Texto originalmente publicado em https://www.infoescola.com/matematica/potenciacao-exponenciacao/