Você já deve ter ouvido falar muito na quantidade de dioptria nas lentes de óculos de uma pessoa, ou diríamos que você já ouviu comumente alguém dizer que: “possuo x graus na lente do olho esquerdo”. A Dioptria é uma unidade de medida que se refere ao poder de refração das lentes em um sistema óptico, ou seja, o famoso “grau” dos óculos popularmente conhecido. Assim temos que 1 grau é igual a 1 dioptria.
Para entendermos melhor como é calculado a dioptria é interessante conhecermos um pouco de curvaturas. Segue abaixo na figura 1 três ilustrações que nos ajudarão a compreender:
Figura 1 – Ilustra um segmento de reta, curva e circunferência de raio (R).
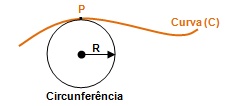
Visivelmente percebemos que a diferença entre o segmento de reta (AB) e a curva (C), é justamente a curvatura, ou seja, para o segmento de reta (AB) a curvatura é igual a zero e a curvatura da curva (C) é diferente de zero. Existe um exemplo de curva mais simples e bem regular: a circunferência, e podemos determinar o valor de sua curvatura utilizando a seguinte equação matemática:
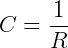(1)
Onde R é o valor do raio da circunferência e C representa o valor da curvatura. Podemos concluir então que a curvatura de uma curva é definida como o inverso do raio, assim temos que o valor de curvatura é menor que 1 e quanto maior for o raio será menor a curvatura.
Agora que sabemos como achar a curvatura de uma circunferência, como faríamos para determinar a curvatura de um determinado ponto em um seguimento como a curva (C)? Simples, para isso devemos posicionar uma circunferência sobre o ponto de uma curva, de modo que “encaixe” exatamente sobre o ponto desejado na curva, pode-se variar o raio para deixando a posição mais correta possível, assim que estiver bem posicionada basta calcular o calor da curvatura do circunferência que será o mesmo valor para a curvatura do ponto.
Figura 2 – Ilustra a sobreposição da circunferência com o ponto (P) da curva (C).
O calculo da dioptria é muito parecido com o da curvatura, no entanto, apenas alteramos o raio da equação (1) para a distância focal (f), assim teremos que a dioptria será o inverso da distância focal da lente, para esse calculo temos que a unidade de medida da dioptria é o inverso do metro (m-1).
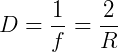(2)
Assim podemos dizer então que, uma lente convergente de distância focal igual a 1 m, terá a potência de 1 dioptria. Se a distância focal for de 0,5 m, a potência será de 2 dioptrias.
O olho de um ser humano tem a distância focal de aproximadamente 17 mm, dependo da deficiência na visão de uma pessoa, existe a necessidade de uma maior ou menor distância focal para que os raios luminosos possam convergir sobre a retina, essa correção é feita com a utilização das lentes.
Figura 3 – Ilustração de um olho com miopia e a correção com lentes bi-côncavos.
No exemplo acima podemos observar um olho com miopia, isso ocorre por um olho anormalmente mais longo, com isso a imagem de forma antes da retina, a utilização das lentes bi-côncavos corrigem essa deficiência formando prolongando a formação das imagens se fixando sobre a retina.
Fontes:
https://web.archive.org/web/20100219221345/http://www.policlin.com.br:80/drpoli/033/
SEARA DA CIÊNCIA - https://web.archive.org/web/20180925065408/http://www.searadaciencia.ufc.br/donafifi/gausseeuler/gausseuler1.htm.
FEIRA DE CIENCIAS - https://web.archive.org/web/20221006145118/http://www.feiradeciencias.com.br/sala24/24_A02.asp
Texto originalmente publicado em https://www.infoescola.com/optica/dioptria/