Conteúdo deste artigo
Número Binomial
Um número binomial, denotado como  , com n e p naturais e
, com n e p naturais e 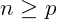 é definido como:
é definido como:
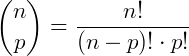
Lemos  como “n classe p” ou “binomial de n sobre p”. O símbolo “!” é chamado Fatorial.
como “n classe p” ou “binomial de n sobre p”. O símbolo “!” é chamado Fatorial.
Assim como nas frações, n é o numerador e p é o denominador.
Binomiais complementares
Dois números binomiais são ditos complementares quando possuem o mesmo numerador e a soma de seus denominadores é igual ao numerador, ou seja,  e
e  são complementares se, e somente se,
são complementares se, e somente se, 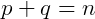 .
.
Quando os denominadores são iguais, os binomiais também são complementares.
Exemplo: 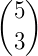 e
e 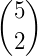 são complementares, pois os numeradores são iguais a 5 e 3 + 2 = 5.
são complementares, pois os numeradores são iguais a 5 e 3 + 2 = 5.
Relação de Stiffel
A relação de Stiffel diz que a soma de dois números binomiais com o mesmo numerador e denominadores consecutivos é igual ao número binomial com uma unidade a mais no numerador e com denominador igual ao maior dos denominadores daqueles binomiais, ou seja:
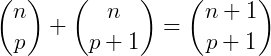
Triângulo de Pascal
Os números binomiais podem ser organizados em uma tabela, de modo que um número binomial  ocupe a linha n e a coluna p formando, assim, o Triângulo de Pascal.
ocupe a linha n e a coluna p formando, assim, o Triângulo de Pascal.
 |
||||||
 |
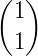 |
|||||
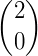 |
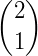 |
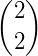 |
||||
 |
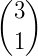 |
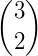 |
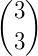 |
|||
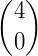 |
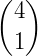 |
 |
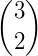 |
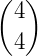 |
||
 |
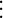 |
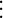 |
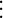 |
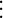 |
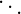 |
|
 |
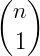 |
 |
 |
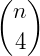 |
... |  |
Cada um dos elementos da coluna 0 é da forma  ou seja, é igual a 1. O último elemento da última linha é da forma
ou seja, é igual a 1. O último elemento da última linha é da forma  , ou seja, também é igual a 1. Ao somarmos dois binomiais consecutivos de uma determinada linha usando a Relação de Stiffel, obtemos o binomial localizado imediatamente abaixo do segundo binomial. Por exemplo,
, ou seja, também é igual a 1. Ao somarmos dois binomiais consecutivos de uma determinada linha usando a Relação de Stiffel, obtemos o binomial localizado imediatamente abaixo do segundo binomial. Por exemplo, 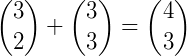 .
.
Desse modo, podemos montar um Triângulo de Pascal utilizando essas regras, com o valor de cada binômio já calculado. Assim, teremos:
| 1 | |||||
| 1 | 1 | ||||
| 1 | 2 | 1 | |||
| 1 | 3 | 3 | 1 | ||
| 1 | 4 | 6 | 4 | 1 | |
| 1 | 5 | 10 | 10 | 5 | 1 |
Teorema das Linhas
A soma dos elementos de cada linha de ordem n é igual a 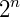 .
.
| Linha 0 | 1 | Soma = 1 = 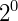 |
|||||
| Linha 1 | 1 | 1 | Soma = 2 = 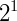 |
||||
| Linha 2 | 1 | 2 | 1 | Soma = 4 = 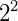 |
|||
| Linha 3 | 1 | 3 | 3 | 1 | Soma = 8 = 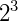 |
||
| Linha 4 | 1 | 4 | 6 | 4 | 1 | Soma = 16 = 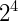 |
Teorema das Colunas
A soma dos números binomiais de determinada coluna, desde o primeiro elemento  até um elemento qualquer
até um elemento qualquer 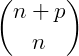 é igual ao número binomial imediatamente abaixo e à direita deste último, ou seja, o número binomial
é igual ao número binomial imediatamente abaixo e à direita deste último, ou seja, o número binomial 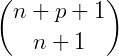 .
.
| 1 | |||||||
| 1 | 1 | ||||||
| 1 | 2 | 1 | |||||
| 1 | 3 | 3 | 1 | ||||
| 1 | 4 | 6 | 4 | 1 | |||
| 1 | 5 | 10 | 10 | 5 | 1 | ||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | |
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 |
1 + 2 + 3 + 4 + 5 = 15
1 + 4 + 10 + 20 = 35
Teorema das transversais
A soma dos números binomiais de determinada transversal, desde o elemento  até um elemento qualquer
até um elemento qualquer 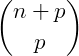 , obtemos o número binomial imediatamente abaixo deste último, ou seja, o número binomial
, obtemos o número binomial imediatamente abaixo deste último, ou seja, o número binomial 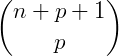 .
.
| 1 | |||||||
| 1 | 1 | ||||||
| 1 | 2 | 1 | |||||
| 1 | 3 | 3 | 1 | ||||
| 1 | 4 | 6 | 4 | 1 | |||
| 1 | 5 | 10 | 10 | 5 | 1 | ||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | |
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 |
1 + 4 + 10 + 20 = 35
Binômio de Newton
Observe o desenvolvimento dos seguintes produtos notáveis.
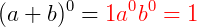
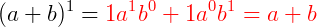
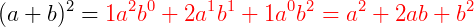
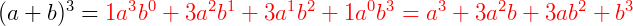
Os coeficientes resultantes do desenvolvimento desses binômios, que estão em vermelho, são os números binomiais que aparecem no Triângulo de Pascal.
| 1 | |||
| 1 | 1 | ||
| 1 | 2 | 1 | |
| 1 | 3 | 3 | 1 |
Cada termo do desenvolvimento do produto notável 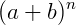 se associa com o desenvolvimento de um binomial no triângulo de pascal.
se associa com o desenvolvimento de um binomial no triângulo de pascal.
Vamos reescrever o desenvolvimento acima usando binomiais, colocando expoentes decrescentes para a e expoentes crescentes para b.
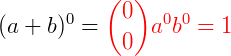
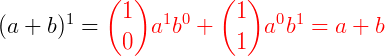
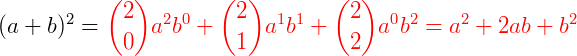
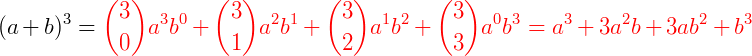
Generalizando, o desenvolvimento de um produto notável 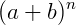 será:
será:
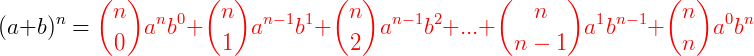
Podemos reescrever esta expressão como um somatório:
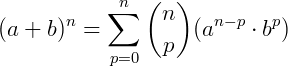
Essa expressão é conhecida como Fórmula do Binômio de Newton.
Exemplo: desenvolver 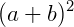 usando a Fórmula do Binômio de Newton.
usando a Fórmula do Binômio de Newton.
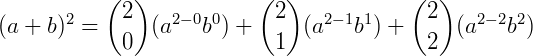
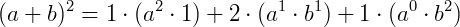
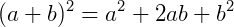
Fórmula do Termo Geral
Como visto anteriormente, 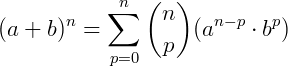 .
.
Observe que o primeiro termo (T1) será obtido fazendo p = 0.
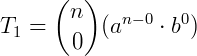
O segundo termo (T2) será obtido quando p = 1:
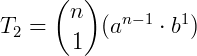
Assim, para encontrar o termo enésimo termo, fazemos p = p+1:
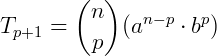
Exemplo:
Qual o coeficiente de b4no desenvolvimento de 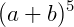 ?
?
p = 4 e n = 5.
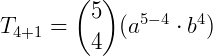
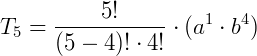
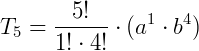
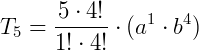
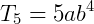
Assim, o coeficiente será 5.
Referências:
PAULO, Luiz. Matemática: Binômio de Newton. Vol. 5. São Paulo: Bernoulli.
HAZZAN, Samuel. Fundamentos de Matemática Elementar. Combinatória. Probabilidade. Vol. 5. São Paulo: Atual, 1997.
Texto originalmente publicado em https://www.infoescola.com/matematica/binomio-de-newton/