Triângulo de Pascal

Para melhor entendimento a respeito das propriedades do Triângulo de Pascal, vamos apresentar o conceito de combinação e coeficientes binomiais.

Imagine o seguinte cenário: Estamos organizando um campeonato de xadrez com 12 participantes. De quantas maneiras possíveis podemos criar as duplas para disputar a primeira partida? Este problema pode ser solucionado calculando a combinação de 12 jogadores organizados de 2 em 2. Que nos traz:

$C_{12,2}=\frac{12!}{2!\cdot (12-2)!}=\frac{12!}{2!\cdot 10!}=\frac{12\cdot 11\cdot 10!}{2!\cdot 10!}=\frac{12\cdot 11}{2}=66$

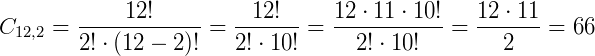
Temos então 66 formas diferentes de organizar as duplas a partir dos 12 primeiros participantes. Há uma outra notação para a operação de combinação, ou coeficiente binomial, que é dada por:

$C_{n,r}=\binom{n}{k}=\frac{n!}{k!\cdot(n-k)!}$

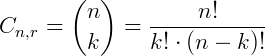
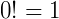O triângulo de Pascal (que na Itália é chamado de triângulo de Tartaglia e na China, triangulo de Yang Hui) é uma construção de números infinitos formado por números binomiais $\binom{n}{k}$ onde n representa o número da linha e k o número da coluna que ele está. Lembrando que $0! = 1$. Temos então:

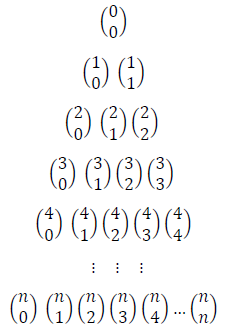
Se desenvolvermos todos os coeficientes binomiais acima obtemos um triângulo composto pelos seguintes números:

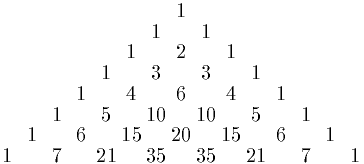
Propriedades interessantes

O triângulo de Pascal possui diversas relações curiosas entre aos seus elementos. Vejamos algumas:

P1) Cada número do triângulo de Pascal é a soma dos dois números acima:

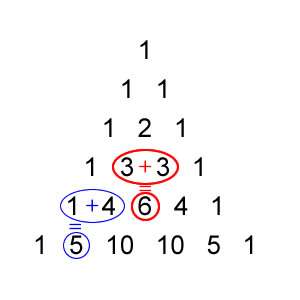Esta propriedade também é chamada de Relação de Stifel, que formalmente pode ser escrita como:

$\binom{n-1}{k-1}+\binom{n-1}{k}=\binom{n}{k}$

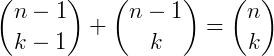
P2) A soma de cada linha nos traz em ordem todas as potências de 2:

$1=2^0$

$1+1=2=2^1$

$1+2+1=4=2^2$

$1+3+3+1=8=2^3$

$1+4+6+4+1=16=2^4$

$1+5+10+10+5+1=32=2^5$

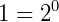
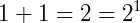
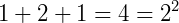
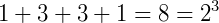
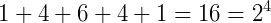
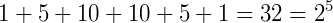
P3) Se escrevermos em ordem cada linha do triângulo de Pascal como se fossem um número único temos todas as potências de 11:

$1=11^0$

$11=11^1$

$121=11^2$

$1.331=11^3$

$14.641=11^4$

$161.051=11^5$

$1.771.561=11^6$

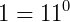
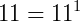
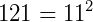
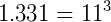
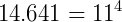
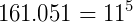
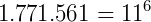
P4) O triângulo de Pascal possui uma simetria entre os seus elementos que nos garante a seguinte igualdade:

$\binom{n}{k}=\frac{n!}{k!\cdot(n-k)!}=\frac{n!}{(n-k)!\cdot k!}=\binom{n}{n-k}$

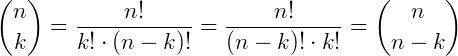
Aplicações - expressão binomial

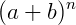Os números da forma $\binom{n}{k}$ aparecem como coeficientes no desenvolvimento de expressões binomiais $(a+b)^n$ e quando for um número inteiro positivo, dizemos que:

$(a+b)^n=(a+b)\cdot(a+b)...(a+b)$

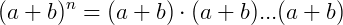
Exemplos:

$(a+b)^1=a+b$

$(a+b)^2=a^2+2ab+b^2$

$(a+b)^3=a^3+3a^2b+3ab^2+b^3$

$(a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4$

$(a+b)^5=a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5$

$(a+b)^6=a^6+6a^5+b+15a^4b^2+20a^3b^3+15a^2b^4+6ab^5+b^6$

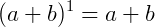
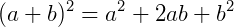
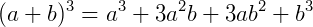
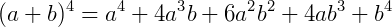
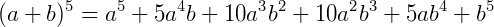
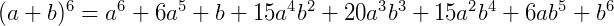
Note os coeficientes obtidos nas expressões binomiais acima. Se reescrevê-los na forma de um triângulo obtemos o triângulo de Pascal.

Quando multiplicamos (a+B) n vezes, cada termo será formado de k elementos a e de (n-k) elementos b, onde k=0, 1, 2, 3...n . Então surge a pergunta: Quantos termos da forma 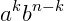$a^kb^{n-k}$ existirão: Simplesmente contaremos o número de maneiras possíveis de escolher k dentre os n elementos a, deixando de lado a ordem, ou seja, isso será justamente dado por $\binom{n}{k}$. Daí obtemos o que é conhecido como o teorema binomial, ou Binômio de Newton:

$\displaystyle (a+b)^n=\sum^{n}_{k=0}\binom{n}{k}a^kb^{n-k}$

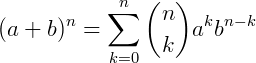
Referências Bibliográficas

MEYER, Paul L. Probabilidade: Aplicações à Estatística. São Paulo: Editora Livros Técnico Científicos, 1975.

]ROONEY, Anne. A História da Matemática. São Paulo: Editora M. Books, 2012.

Texto originalmente publicado em https://www.infoescola.com/combinatoria/triangulo-de-pascal/