Ângulos

O estudo dos ângulos é fundamental para compreender conceitos ligados a geometria, trigonometria, entre outros ramos da Matemática. O estudo dos ângulos é um dos responsáveis pelos avanços que possuímos atualmente em vários ramos, como a navegação e a astronomia. Um exemplo notável é o astrolábio náutico (inventado pelo grego Hiparco) usado para medir ângulos. Nos séculos V e VI, os navegadores construíram esse instrumento para medir a elevação das estrelas e do sol com o intuito de localizar suas embarcações. Mais tarde, o astrolábio deu origem ao sextante, mais simplificado, mas que cumpria a mesma função.

Definição de ângulo

Chama-se ângulo a região entre duas semirretas que partem de uma mesma origem. Podemos dizer, ainda que um ângulo é a medida da abertura de duas semirretas que partem da mesma origem.

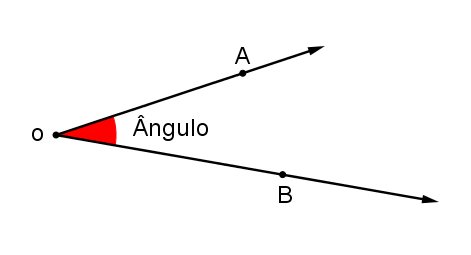
Indica-se: ∠AOB, ∠BOA, AÔB, BÔA ou Ô.

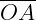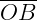O ponto "O" é o vértice do ângulo e as semirretas $\overline{OA}$ e $\overline{OB}$ são os lados do ângulo.

Ângulos consecutivos

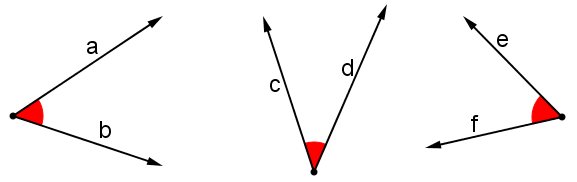
Dois ângulos são consecutivos se eles compartilham um mesmo lado, ou seja, se o lado de um, for também o mesmo lado do outro.

Ângulos adjacentes

Dois ângulos consecutivos são adjacentes se, e somente se, não compartilham pontos internos, ou seja, não estão sobrepostos um ou outro.

Congruência (≅)

Para que ângulos possam ser considerados congruentes (iguais), devem satisfazer os seguintes postulados:

1. reflexiva: todo ângulo é congruente a si mesmo (aôb ≅ aôb)
2. simétrica: se aôb ≅ côd, então côd ≅ aôb
3. transitiva: se aôb ≅ côd e côd ≅ eôf então aôb ≅ eôf

Adição de ângulos

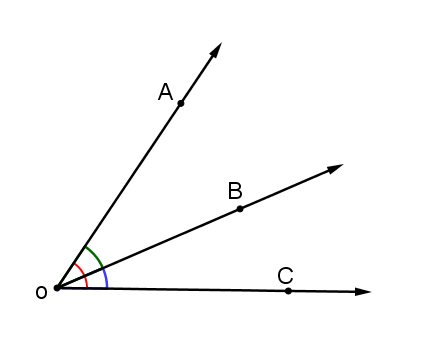
Se a semirreta OB é interna ao ângulo AÔC, o ângulo AÔC é a soma dos ângulos AÔB e BÔC. Assim:

AÔC = AÔB + BÔC

Bissetriz de um ângulo

A bissetriz de um ângulo é a semirreta que parte do vértice do ângulo e o divide em dois ângulos congruentes (iguais).

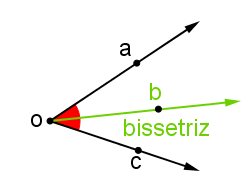
Formalmente falando, uma semirreta ob interna ao ângulo aôc, é bissetriz desse ângulo se, e somente se, aôb ≅ bôc.

Ângulos opostos pelo vértice

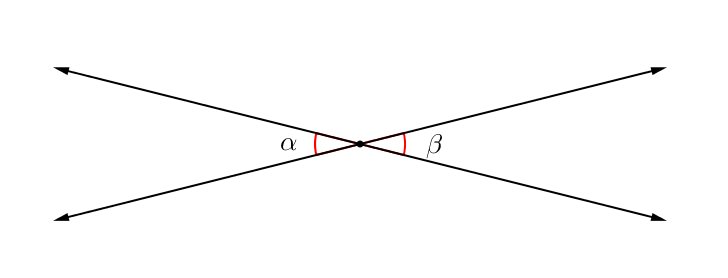
Dizemos que dois ângulos são opostos pelo vértice se as semirretas que os formam partem do mesmo vértice e são opostas aos lados do outro.

$\alpha = \beta$

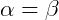
Medida de um ângulo - amplitude

A medida de um ângulo é um número real positivo associado a ele, de forma que:

1. Ângulos congruentes têm medidas iguais e ângulos iguais são congruentes.
2. Se um ângulo α é maior que um ângulo β, então a medida de α será maior que a medida de β.
3. A soma de dois ou mais ângulos é a soma das medidas de cada um desses ângulos.

Chamamos a medida de um ângulo de amplitude.

Unidades de medida de um ângulo

Grau (°)

A unidade principal de medida de um ângulo é o grau (°).

1° (um grau) equivale a 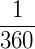$\frac{1}{360}$ de uma circunferência, ou seja, 1° corresponde a uma das 360 partes em que uma circunferência foi dividida. Assim, uma circunferência inteira possui 360°.

Minuto ( ‘ )

Quando queremos expressar medidas de ângulos menores que 1°, utilizamos a medida minuto ( ‘ ). Um minuto corresponde a 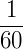$\frac{1}{60}$ de um grau, ou seja, 1 minuto (1’) corresponde a uma das 60 partes em que um ângulo de 1° foi dividido.

$1^{\prime} = \frac{1^o}{60}$

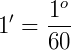
Um grau possui 60 minutos (1º = 60').

Segundo ( '' )

Quando queremos expressar medidas de ângulos menores que 1°, utilizamos a medida segundo ( '' ). Um segundo corresponde a 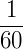$\frac{1}{60}$ de um minuto, ou seja, 1 segundo (1'') corresponde a uma das 60 partes em que um ângulo de 1' foi dividido.

$1^{\prime\prime} = \frac{1^{\prime}}{60}$

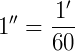
Um minuto possui 60 segundos (1' = 60'').

Grado

Esta medida não é muito usual.

Um grado corresponde a 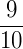$\frac{9}{10}$ de um grau, ou seja, 1 grado (1 gr) corresponde a 9 das 10 partes em que um ângulo de 1° foi dividido.

Classificação de ângulos

Os ângulos podem ser classificados de acordo com a sua medida.

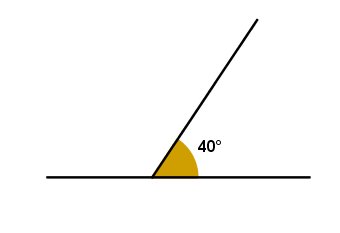
Ângulo agudo: ângulo com medida menor que 90º (0° < α < 90°).

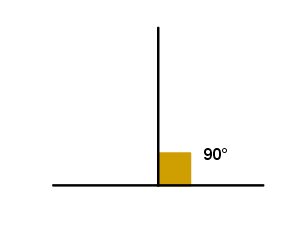
Ângulo reto: ângulo com medida igual a 90º.

Ângulo obtuso: ângulo com medida maior que 90º (90° < α < 180°).

Ângulo raso: ângulo com medida igual a 0º ou 180º.

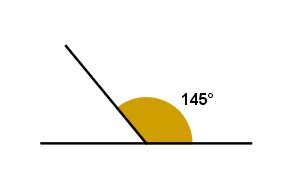
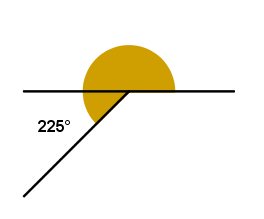
Ângulo Côncavo: ângulo com medida entre 180º e 360º.

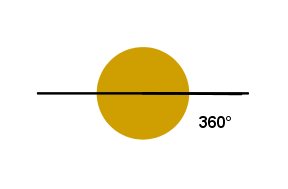
Ângulo completo ou de uma volta: ângulo com medida igual a 360°.

Ângulos complementares

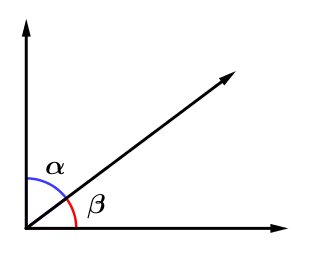
Dizemos que dois ângulos são complementares quando a sua soma equivale a 90°.

$\alpha + \beta = 90^o$

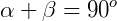
Ângulos suplementares

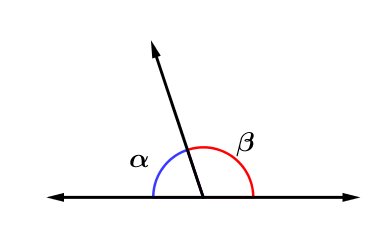
Dizemos que dois ângulos são suplementares se, e somente se, a sua soma for igual a 180°.

$\alpha + \beta = 180^o$

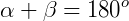
Ângulos replementares

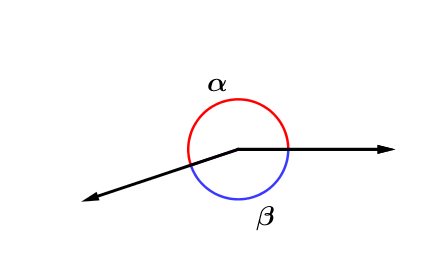
Dois ângulos são replementares quando a sua soma for igual a 360°.

$\alpha + \beta = 360^o$

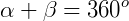
Retas paralelas cortadas por uma transversal

Duas retas paralelas e distintas, r e s, cortadas por uma outra reta transversal t delimitam oito ângulos, como na figura. Esses ângulos serão suplementares ou congruentes.

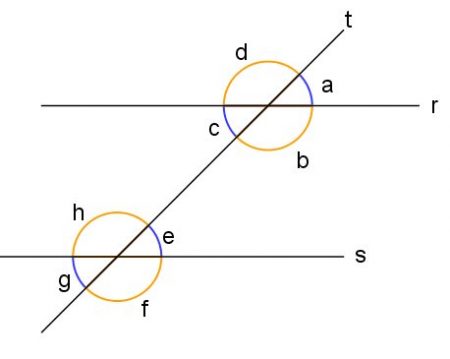
Nesses casos, podemos atribuir alguns nomes especiais, veja:

Correspondentes: 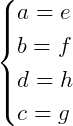$\begin{cases}a = e \\ b = f \\ d = h \\ c = g \end{cases}$

Alternos: 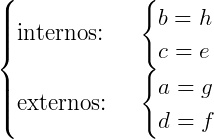 $\begin{cases}\text{internos: } &\begin{cases}b = h \\ c = e \end{cases} \\ \text{externos: } &\begin{cases}a = g \\ d = f \end{cases}\end{cases}$

Colaterais: 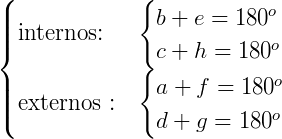$\begin{cases}\text{internos: } &\begin{cases} b+e = 180^o \\ c+h = 180^o \end{cases} \\ \text{externos :} &\begin{cases} a+f = 180^o \\ d+g = 180^o \end{cases} \end{cases}$

Exemplos

1. Um ângulo excede o seu complemento em 48°. DETERMINE o suplemento desse ângulo.

Seja x o ângulo procurado e y o seu complemento. x = 48 + y. Como x e y são complementares, x + y = 90. Assim, y = 90 – x. Então

x = 48+(90-x)

x = 48+90-x

x = 138-x

2x = 138

x = 138/2 = 69º

Então, 69° somado com seu suplemento deve ser igual a 180°. Assim, o suplemento será 180°- 69° = 111°.

2. (FUVEST-SP). Na figura a seguir, as retas r e s são paralelas, o ângulo 1 mede 45° e o ângulo 2 mede 55°. A medida, em graus, do ângulo 3 é:

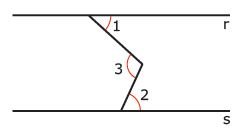
• A) 50
• B) 55
• C) 60
• D) 80
• E) 100

Traçando uma reta paralela as retas r e s, cortando o ângulo 3, temos:

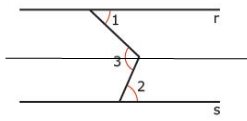
Agora, o ângulo 3 está dividido em dois outros ângulos.

Note que os ângulos 1 e a parte superior do ângulo 3 são ALTERNOS INTERNOS, ou seja são iguais. Assim, a parte superior do ângulo 3 é igual a 45°

O mesmo acontece com os ângulos 2 e a parte inferior do ângulo 3. Assim, o ângulo inferior de 3 será igual a 55°

Juntando os dois ângulos, teremos o ângulo 3.

Assim, o ângulo 3 mede 45°+55° = 100°

Alternativa E.

Referências:

DOLCE, Osvaldo; POMPEO, José Nicolau. Fundamentos de Matemática Elementar. Geometria Plana. Vol. 9. São Paulo: Atual, 1995.

RIBEIRO, Paulo Vinícius. Matemática: Noções primitivas de geometria plana. Vol. 1. São Paulo: Bernoulli.

Texto originalmente publicado em https://www.infoescola.com/matematica/angulos/