Equações Diferenciais de Primeira Ordem

Equações diferenciais são ferramentas importantes para diversos ramos das ciências exatas. Com elas é possível descrever e formular diversos tipos de sistemas físicos numa linguagem matemática, o que possibilita uma imensa gama de aplicações em modelos concretos. Relembrando brevemente a notação para derivadas, temos:

$\frac{dy}{dx}=y'(x)$

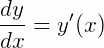
Recomenda-se ao leitor que leia o artigo sobre Equações Diferenciais.

Equações diferenciais ordinárias de primeira ordem

A ordem da mais alta derivada envolvida em uma ED é chamada de sua ordem. No caso de uma ED de 1ª ordem, sua ordem é igual a 1. A equação abaixo é uma EDO de primeira ordem:

$4x\frac{dy}{dx}-2y=x$

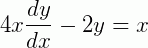
Solução de uma EDO

É chamada de solução de uma ED qualquer função definida em algum intervalo que quando substituída na ED, reduz a equação a uma identidade. De uma forma geral para as EDOs, temos:

$F(x, y, y', ..., y^{(n)})=F(x, f(x), f(x)', ..., f(x)^{(n)})=0$

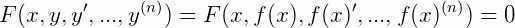
Que F é uma função que possui pelo menos n derivadas e satisfaz a equação diferencial. Vejamos um exemplo:

Seja uma EDO de 1º grau dada por:

$\frac{dy}{dx}=x\sqrt{y}$

E vamos verificar se 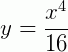$y=\frac{x^4}{16}$ é uma solução para a EDO. Primeiro, podemos substituir o valor dado na equação, ou seja, o valor de y da solução deverá ser inserido na EDO:

$\frac{dy}{dx}=x\sqrt{\frac{x^4}{16}}=x\frac{x^2}{4}=\frac{x^3}{4}$

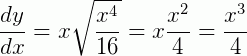
Agora, se reinserirmos o valor obtido pela igualdade acima na EDO, percebemos que:

$\frac{dy}{dx}-x\sqrt{y}=0$

$\frac{x^3}{4}-x\sqrt{\frac{x^4}{16}}=0$

$\frac{x^3}{4}-\frac{x^3}{4}=0$

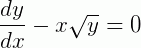
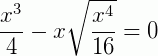
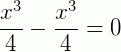
O que prova que o valor de y dado é solução da EDO.

Problema de Valor Inicial (PVI)

É chamado de problema de valor inicia quando queremos resolver uma EDO de 1ª ordem, do tipo:

$\frac{dy}{dx}=f(x, y)$

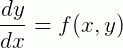
Que está sujeita a uma condição inicial que chamaremos de 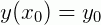$y(x_0)=y_0$, em que x₀ é um número qualquer dentro de um intervalo I e y₀ é um número real.

Agora, um exemplo prático. Seja a EDO de 1ª ordem dada por:

$y'=y-y^2$

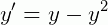
Leve em conta que existe uma família de soluções parâmetro para esta equação que será dada por:

$y(x)=\frac{1}{(1+Ce^{-x})}$

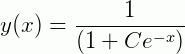
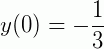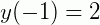Vamos determinar o seu PVI para os casos onde $y(0)=-\frac{1}{3}$ e $y(-1)=2$. Sendo assim:

$y(0)=\frac{1}{(1+Ce^0)}=\frac{-1}{3}\quad C_1=-4$

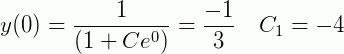
E para o segundo caso:

$y(-1)=\frac{1}{(1+Ce)}=2\quad C_2=\frac{-1}{2e}$

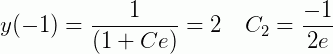
Isto significa que esta EDO possui pelo menos duas soluções. Quando reinserimos os valores na EDO, obtemos:

$y(x)=\frac{1}{(1+C_1e^{-x})}=\frac{1}{(1-4e^{-x})}$

$y(x)=\frac{1}{(1+C_2e^{-x})}=\frac{1}{(1-\frac{e^{-x}}{2e})}$

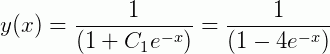
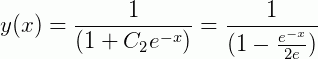
Para continuarmos o estudo das EDOs de 1ª ordem, os artigos Equações Diferenciais Separáveis e Equações Exatas e Lineares serão importantes para melhor compreensão de como solucionar EDOs bem como alguns métodos de solução.

Referências bibliográficas:

ZILL, Dennis G; CULLEN, Michael R. Equações Diferenciais – Volume 1. São Paulo – Pearson Makron Books, 2001.

BASSALO, José Maria FIlardo; CATTANI, Mauro Sérgio Dorsa. Elementos de Física Matemática – Volume 1. São Paulo – Livraria da Física, 2010.

ARFKEN, George B; WEBER, Hans J; HARRIS, Frank E. Física Matemática: Métodos Matemáticos para Engenharia e Física – 7a Ed. Rio de Janeiro: Elsevier, 2017.

Texto originalmente publicado em https://www.infoescola.com/matematica/equacoes-diferenciais-de-primeira-ordem/