Fatoração

Fatorar uma expressão algébrica ou um polinômio significa transformar a expressão algébrica ou o polinômio, num produto de fatores irredutíveis. Assim, por exemplo, cada uma das identidades abaixo pode ser analisada sob dois aspectos distintos:

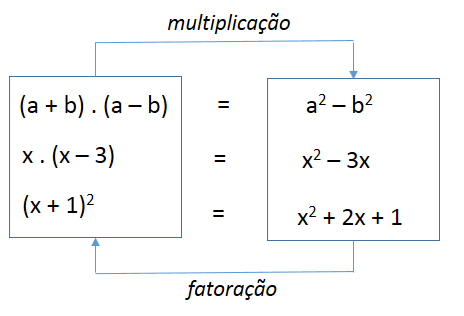
a) da esquerda para a direita, efetuamos a multiplicação indicada no 1º membro;

b) da direita para a esquerda, foi feita a fatoração da expressão que aparece no 2º membro, ou seja, ela foi transformada em um produto de fatores de grau menor.

Nesse sentido, podemos dizer, de modo geral, que fatorar é o “caminho inverso” de multiplicar.

Em seguida, vamos apresentar os principais casos de fatoração.

1º caso: colocar fator comum em evidência

Este caso se baseia na propriedade distributiva da multiplicação em relação à adição e subtração:

ab + ac – ad = a . (b + c – d)

Dizemos que o fator a, comum a todos os termos do 1º membro, foi colocado em evidência.

De maneira geral, ao fatorar um polinômio, colocamos em evidência o máximo divisor comum (MDC) de seus termos e, em seguida, dividimos cada termo por esse MDC.

Exemplos:

1. Fatore a expressão 5x + 5y – 5z.

Nesse caso, é fácil identificar o fator em comum: 5. Como estamos fazendo o processo inverso da propriedade distributiva da multiplicação, podemos dividir cada termo pelo fator comum para encontrar a forma fatorada:

$5x+5y-5z=$

$5\cdot\left(\frac{5x}{5}+\frac{5y}{5}-\frac{5z}{5}\right)=$

$5\cdot(x+y+z)$

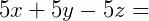
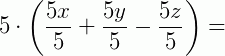
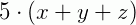
2. Fatore a expressão 3x³y² – 6x⁴y³ + 12 x⁶y⁴.

Podemos reescrever a expressão 3x³y² – 6x⁴y³ + 12 x⁶y⁴ como 3x³y² – 6.x³. x.y².y + 12.x³.x³.y².y²

Observe que 3.x³.y² é o fator comum. Colocando-o em evidência, temos:

$3x^3y^2-6x^2y^3+12x^6y^4=$

$3x^3y^2\cdot\left(\frac{3x^3y^2}{3x^3y^2}-\frac{6x^4y^3}{3x^3y^2}+\frac{12x^6y^4}{3x^3y^2}\right)=$

$3x^3y^2\cdot(1-2xy+4x^3y^2)$

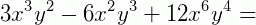
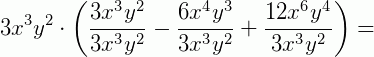
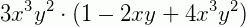
3. Fatore a expressão 7ab²y² – 21a²b²m + 28a³b⁴.

Reescrevendo a expressão, temos: 7.a.b²y² – 7.3.a.a.b².m + 7.4. a.a².b²b²

Observe que 7.a.b² é o fator comum . Colocando-o em evidência, temos:

$7ab^2y^2-21a^2b^2m+28a^3b^4=$

$7ab^2\cdot\left(\frac{7ab^2y^2}{7ab^2}-\frac{21a^2b^2m}{7ab^2}+\frac{28a^3b^4}{7ab^2}\right)=$

$7ab^2\cdot(y^2-3am+4a^2b^2)$

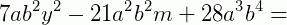
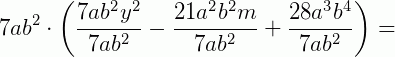
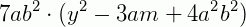
2º caso: Agrupamento

Este caso se aplica quando:

a) não existe um fator comum para todas as parcelas;

b) partes da expressão (grupos) possuem fator comum.

Nesse caso, formamos dois ou mais grupos com um termo comum. Em seguida, colocamos em evidência um fator comum a todos os grupos.

Exemplos:

1. Fatore a expressão x² + ax + bx + ab

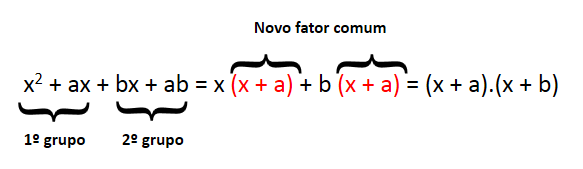
Portanto: x² + ax + bx + ab = (x + a) . (x + b)

2. Fatore a expressão 2ax² + 3axy – 2bxy – 3by²

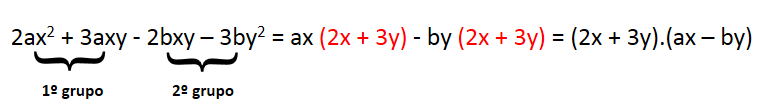
Portanto: 2ax² + 3axy – 2bxy – 3by² = (2x + 3y) . ( ax – by)

3. Fatore a expressão axy + bcxy – az – bcz – a – bc

Portanto: 2ax² + 3axy – 2bxy – 3by² = (a + bc) . ( xy –z – 1)

3º caso: Diferença de quadrados

A partir da propriedade simétrica da igualdade (se a = b, então b = a), pode-se dizer que:

se (x + y)(x – y) = x² – y², então x² – y² = (x + y)(x – y)

Observando que, esse binômio é composto pela diferença do quadrado de dois termos, podemos fatorá-lo facilmente, escrevendo-o como produto da soma pela diferença desses termos.

Exemplos:

1. Fatore a expressão x² - 16

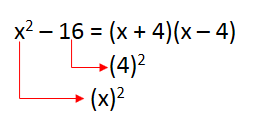
2. Fatore a expressão 16x⁴ – 25b²

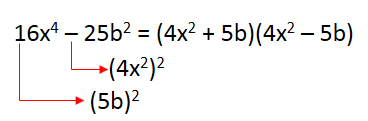
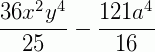
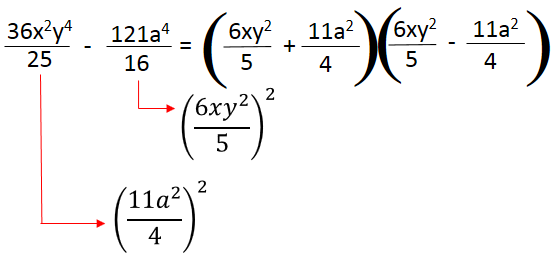
3. Fatore a expressão $\frac{36x^2y^4}{25}-\frac{121a^4}{16}$

4º caso: Trinômio quadrado perfeito

Todo polinômio com três termos que apresenta dois monômios quadrados perfeitos (a² e b²), cujo terceiro termo é igual a duas vezes o produto das bases desses monômios quadrados perfeitos, em módulo ( 2ab), é um trinômio quadrado perfeito, isto é, pode ser reduzido a uma das seguintes formas:

a² + 2ab + b² = (a + b)² ou a² -2ab + b² = (a – b)²

Exemplos:

1. Verifique se o trinômio x² + 4x + 4 a seguir são quadrados perfeitos e, caso sejam, fatore-os.

Escrevendo o primeiro e o terceiro como quadrados, temos:

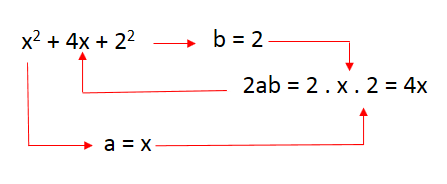
Como 2ab é igual ao termo 4x, o trinômio é quadrado perfeito:

2ab = 2 . x . 2 = 4x (logo, x² + 4x + 4 é quadrado perfeito)

Fatorando o trinômio, temos: x² + 4x + 4 = (x + 2)²

2. Verifique se o trinômio 4x² - 20x + 5² a seguir são quadrados perfeitos e, caso sejam, fatore-os.

Escrevendo o primeiro e o terceiro como quadrados, temos:

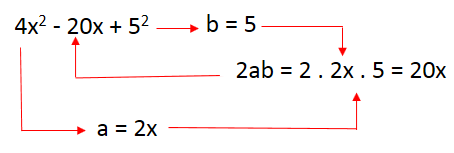
Como 2ab é igual ao termo 20x, o trinômio é quadrado perfeito e sua forma fatorada é:

4x² - 20x + 25 = (2x - 5)²

5º caso: Trinômio do segundo grau

Mesmo um trinômio não sendo quadrado perfeito, é possível fatorá-lo. Para isso, basta associá-lo a uma equação do 2º grau e conhecer suas raízes. Para um trinômio do tipo ax² + bx + c (a ≠ 0), a equação associada a ele é ax² + bx + c = 0 (a ≠ 0), na qual suas raízes x₁ e x₂ satisfazem as relações:

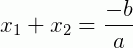$x_1+x_2=\frac{-b}{a}$ e $x_1\cdot x_2=\frac{c}{a}$

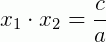
A forma fatorada do trinômio do segundo grau, usando as raízes x₁ e x₂ , é o produto do coeficiente a por dois fatores de 1º grau

ax² + bx + c = a . (x – x₁) . (x – x₂)

Exemplos:

1. Fatore: x² – 5x + 6 (a = 1, b = -5, c = 6)

Calculando as raízes: Δ = b² – 4.a.c = (-5)² – 4.(1).(6) = 25 – 24 = 1

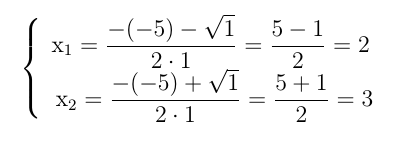
Como x₁ = 2 e x₂ = 3 e a = 1, a forma fatorada do trinômio é: x² – 5x + 6 = 1 (x -2).(x -3)

2. Fatore: 3x² – 2x - 1 (a = 3, b = -2, c = -1)

Calculando as raízes: Δ = b² – 4.a.c = (-2)² – 4.(3).(-1) = 4 + 12 = 16

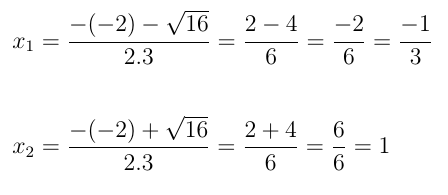
Como 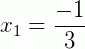$x_1=\frac{-1}{3}$ e x₂ = 1 e a = 3, a forma fatorada do trinômio é:

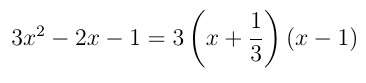
Referências bibliográficas:

1. LIMA, Elon Lages; CARVALHO, Paulo C. P.; WAGNER, Eduardo; MORGADO, Augusto C. A Matemática do Ensino Médio. vol. 3. Coleção do Professor de Matemática, SBM, 2012.

2. IEZZI, G.. Fundamentos De Matemática Elementar . Volume 6. 7ed. São Paulo: Atual Editora, 2004.

3. NETO, Antônio C. Muniz. Tópicos de Matemática Elementar, volume 1: Números Reais. Rio de Janeiro, Editora SBM, 2013.

Texto originalmente publicado em https://www.infoescola.com/matematica/fatoracao/