Uma função (ou aplicação) f: A → B é dita sobrejetora (também chamada de sobrejetiva ou sobrejeção) quando, para todo 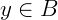 existe pelo menos um
existe pelo menos um 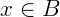 tal que f(x) = y. Em linguagem matemática escrevemos:
tal que f(x) = y. Em linguagem matemática escrevemos:
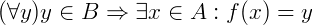
Lê-se: Para qualquer y, onde y pertence ao conjunto B, então existe x pertencente ao conjunto A tal que f(x) = y.
Em outras palavras, quando qualquer elemento de B é imagem de x algum de A, ou que o conjunto imagem é igual ao contradomínio, então Im(f) = B. E, do contrário, dizemos que uma função não é sobrejetiva quando:
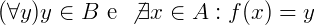
Lê-se: Existe y, onde y pertence ao conjunto B, então não existe x pertencente ao conjunto A tal que f(x) = y.
Ou seja, quando existe um elemento de B que não é imagem de elemento algum de A.
Exemplo 1) Sejam os conjuntos A = {a, b, c, d} e o conjunto B = {x, y, z}, dizemos que a aplicação f = {{(a, x); (b, y); (c, y); (d, z)} é sobrejetora de A em B.
No diagrama podemos representar esta aplicação como:
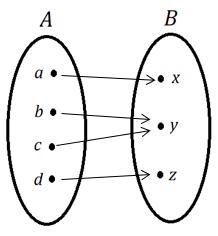
Podemos observar no diagrama acima que a aplicação não é injetora pois 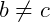 e
e 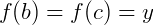 .
.
Exemplo 2) Seja a função 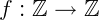 dada por f(x) = x+1. Nesta função, o conjunto imagem é igual ao seu contradomínio, ou seja,
dada por f(x) = x+1. Nesta função, o conjunto imagem é igual ao seu contradomínio, ou seja, 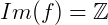 . Perceba que para qualquer valor de x, o seu valor correspondente em y também é um número inteiro. O que caracteriza uma função sobrejetora.
. Perceba que para qualquer valor de x, o seu valor correspondente em y também é um número inteiro. O que caracteriza uma função sobrejetora.
Leia também:
Referências Bibliográficas:
LIMA, Elon Lages. Um Curso de Análise: Volume 1. Rio de Janeiro: IMPA, 2017.
DOMINGUES, Hygino H; IEZZI, Gelson. Álgebra Moderna. São Paulo: Editora Atual, 1982.
Texto originalmente publicado em https://www.infoescola.com/matematica/funcao-sobrejetora/