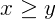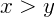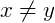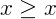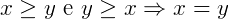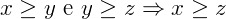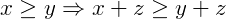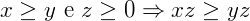Inequação do primeiro grau

Quando estudamos equações do 1º grau lidamos com igualdades, ou seja, expressões em que precisamos encontrar um valor para a variável em questão. Porém, quando tratamos de uma inequação a nossa expressão conterá, ao invés do sinal de igual (=), outros sinais que determinarão uma relação de ordem entre os seus elementos. Geralmente, o conjunto solução de inequações será definido no conjunto dos números Reais. Abaixo as desigualdades e relações de ordem de números Reais:

• Se $x\geq y$, dizemos que x é maior ou igual a y;
• Se $x>y$, então x é maior do que y;
• Se $x\neq y$, dizemos que x é diferente de y.

Agora, algumas propriedades a respeito das desigualdades:

• Reflexiva: $x\geq x$
• Antissimétrica: $x\geq y\text{ e }y\geq x\Rightarrow x=y$
• Transitiva: $x\geq y\text{ e }y\geq z\Rightarrow x\geq z$
• Compatibilidade com a Adição: $x\geq y\Rightarrow x+z\geq y+z$
• Compatibilidade com a Multiplicação: $x\geq y\text{ e }z\geq 0\Rightarrow xz\geq yz$

Exemplo 1) Tomemos agora x, y, z e w, quaisquer números Reais e vamos descobrir se há uma relação de ordem entre eles dados 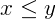$x\leq y$ e $z\leq w$.

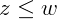Pela compatibilidade com a adição podemos dizer que:

$x\leq y \Rightarrow x+z\leq y+z$

$z\leq w \Rightarrow y+z\leq y+w$

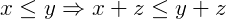
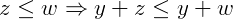
Agora, pela propriedade transitiva temos:

$\left.\begin{aligned}x+z\leq y+z\\y+z\leq y+w\end{aligned}\right\} \Rightarrow x+z\leq y+w$

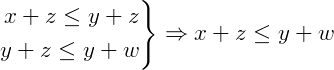
Concluindo:

$\left.\begin{aligned}x\leq y\\z\leq w\end{aligned}\right\} \Rightarrow x+z\leq y+w$

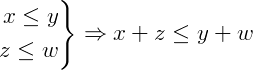
Resolvendo equações do primeiro grau

Exemplo 2) Vamos resolver a equação: 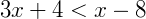$3x+4<x-8$, inicialmente solucionamos como uma equação do primeiro grau comum, isolando as variáveis conservando a regra de sinais:

$3x-x<-4-8$

$2x<-12$

$x<-\frac{12}{2}$

$x<-6$

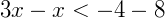
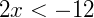
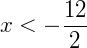
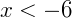
Sendo assim, o conjunto solução da equação será:

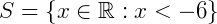
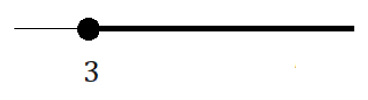
A solução também pode ser escrita na notação de intervalos reais ou representado na reta real como:

$S=]-\infty,-6[$

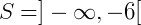
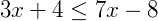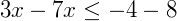
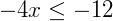
Exemplo 3) Agora, note a solução da equação $3x+4\leq 7x-8$:

$3x-7x\leq -4-8$

$-4x\leq -12$

Perceba que neste ponto, ambos os lados da desigualdade estão negativos. Convenientemente, podemos trocar o sinal de ambos os lados da igualdade multiplicando toda a expressão por (-1). Mas, numa desigualdade, quando invertemos o sinal de toda a expressão, também invertemos a desigualdade, o que nos leva a:

$4x\geq 12$

$x\geq\frac{12}{4}$

$x\geq 3$

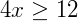
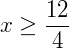
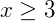
Escrevendo então o conjunto solução desta equação nas três possíveis representações temos:

$S=\{x\in\mathbb{R}:x\geq 3\}$

$S=[3,+\infty[$

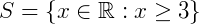
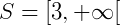
Estudando sinais de inequações

Estudar sinais de inequações permite saber todas as possibilidades para determinar o valor de variáveis em uma expressão. Veja os exemplos abaixo:

Exemplo 4) Vamos estudar o sinal da expressão x-4. Note que esta expressão não está definida em uma igualdade ou desigualdade. Podemos dizer então que existem três possibilidades, são elas:

$\begin{cases}x-4>0 \Rightarrow x>4\\x-4<0 \Rightarrow x<4\\x-4=0 \Rightarrow x=4\end{cases}$

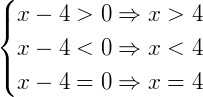
Escolhendo valores maiores, menores ou iguais a 4, vemos que o seu sinal sofrerá mudanças à medida que variarmos o valor de x. Supondo que escolha um valor de x que seja menor do que 4, por exemplo, 3. Pela expressão teríamos:

$x-4 \Rightarrow 3-4= -1$

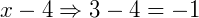
Então, para qualquer valor menor do que quatro, o resultado da expressão será sempre um número negativo. Agora um valor maior que 4, pode ser o 5:

$x-4 \Rightarrow 5-4= 1$

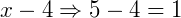
Qualquer valor maior do que 4 a expressão resultará sempre em um número positivo. E se o valor de x fosse 4, teríamos o zero:

$x-4 \Rightarrow 4-4= 0$

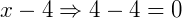
Por fim, se analisarmos o resultado obtido pelo nosso estudo de sinal na reta real, chegaríamos à seguinte representação:

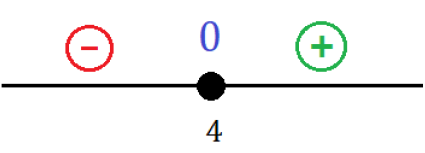
O que significa que qualquer valor à direita da reta sempre nos retornaria um valor positivo, à esquerda valores negativos e quando x for 4 a expressão será igual a zero.

Exemplo 5) Existem algumas inequações onde, para obtermos uma solução, é necessário estudar o comportamento do sinal. Vamos solucionar a inequação 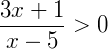$\frac{3x+1}{x-5}>0$:

Como esta inequação está na forma de uma fração, devemos inicialmente estudar o sinal dos dois termos separadamente assim como fizemos no exemplo 4 e depois comparar as análises com a inequação completa:

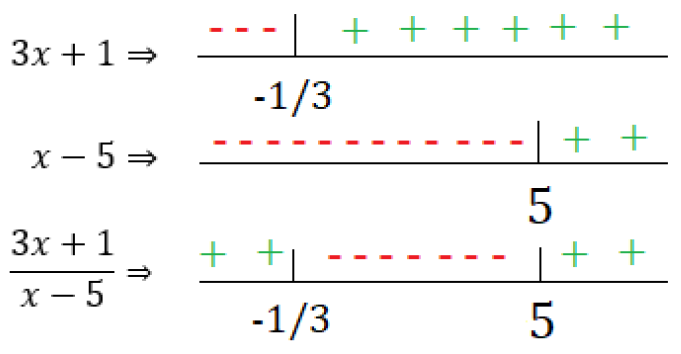
Como a nossa inequação originalmente era 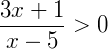$\frac{3x+1}{x-5}>0$ vemos que após o estudo do sinal, nossa solução não estará entre 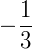$-\frac{1}{3}$ e 5, pois neste intervalo qualquer valor de x terá valor negativo. Substituindo o valor de x na equação original por 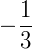$-\frac{1}{3}$ temos:

$\frac{3\cdot\left(-\frac{1}{3}\right)+1}{-\frac{1}{3}-5}=\frac{0}{-\frac{1}{3}-5}=0$

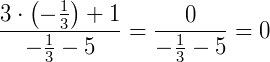
A nossa inequação originalmente dizia quer o valor da expressão deve ser maior do que zero, logo 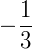$-\frac{1}{3}$ não estará contido no nosso conjunto solução. Vamos agora substituir por 5:

$\frac{3\cdot(5)+1}{5-5}=\frac{16}{0}=\not\exists$

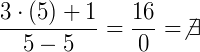
Então, 5 também não estará contido no intervalo do conjunto solução. Por fim, a solução para esta equação será:

$S=\{x\in\mathbb{R}:x<-\frac{1}{3}\text{ ou }x>5\}$

$S=]-\infty,-\frac{1}{3}[\cup]5,+\infty[$

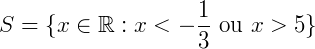
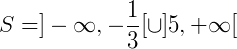
Referências Bibliográficas:

LIMA, Elon Lages. Um Curso de Análise: Volume 1. Rio de Janeiro: IMPA, 2017.

GUIDORIZZI, Hamilton L. Um Curso de Cálculo: Volume 1. Rio de Janeiro: Editora LTC, 2001.

Texto originalmente publicado em https://www.infoescola.com/matematica/inequacao-do-primeiro-grau/