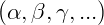O estudo da geometria está repleto de definições. Estas definições estabelecem propriedades, conceitos e entidades muito importantes. Porém, existem noções primitivas que dispensam o uso de definições, dentre elas, os conceitos de ponto, reta e plano. Podemos intuitivamente identificar essas entidades apenas com uma experiência observacional. As noções apresentadas neste artigo terão como base o espaço tridimensional.
Ponto
Um ponto, propriamente dito, é uma entidade que é caracterizada pelos seguintes postulados:
- O ponto não tem dimensão. Ele pode ser, por exemplo, um toque da caneta no papel. Representamos pontos no espaço sempre com letras maiúsculas (A, B, P, M, ...), exemplo:

- Por um ponto no espaço, passam infinitas retas.
- Todo ponto que pertence a uma reta divide-a em duas semirretas, das quais o ponto é a origem.
Reta
A reta também possui postulados:
- Uma reta não tem origem e nem extremidade. É representada sempre por letras minúsculas (r, s, t, u, ...)
- Uma reta é ilimitada e infinita, logo não é possível determinar o seu comprimento.
- Uma reta é um conjunto de infinitos pontos.
- Dois pontos distintos determinam ou individualizam uma reta.

Quando escolhemos como referência um ponto numa reta , ela fica dividida em dois conjuntos de pontos. Cada um desses conjuntos de pontos recebe o nome de semirreta ou raio.
Plano
Outro conceito primitivo que é caracterizado pelos seus postulados.
- Um plano pode ser formado por 3 pontos não colineares. É representado por letras gregas minúsculas
 .
. - Ou por uma reta e um ponto fora dela. Não se esqueça que lidamos com o espaço, então este postulado é possível.
- Um plano pode ser formado por duas retas concorrentes.
- Ou também por duas retas paralelas distintas.

Referências Bibliográficas:
DOLCE, Osvaldo; POMPEO, José Nicolau. Fundamentos de Matemática Elementar. Volume 10: Geometria Espacial. São Paulo: Editora Atual, 2010.
WINTERLE, Paulo. Vetores e Geometria Analítica. São Paulo: Pearson Makron Books, 2000.
Texto originalmente publicado em https://www.infoescola.com/matematica/ponto-reta-e-plano/