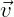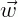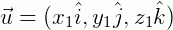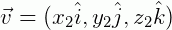Vetores

Dentro do estudo de ciências e matemática existem objetos que são determinados apenas por grandezas numéricas (módulo ou tamanho), e são conhecidos por escalares. São grandezas escalares, por exemplo, o tempo, a temperatura, massa, volume, distância, etc. Por outro lado, existem objetos que além da grandeza numérica (módulo ou tamanho) necessitam da especificação da direção e sentido para que sua definição esteja completa, estes objetos são chamados vetores. Exemplos de grandezas vetoriais: velocidade, aceleração, força, campo elétrico, campo magnético, etc.

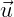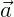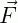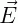Simbolicamente representamos o vetor com uma letra, normalmente minúscula (a menos que a grandeza seja representada com uma letra maiúscula, ex. força e campo elétrico), com uma seta sobre a letra. Por exemplo: $\vec{u}$, $\vec{a}$, $\vec{F}$ ou $\vec{E}$. Já a representação geométrica dos vetores é feita através de um segmento de reta orientado, como mostrado na figura abaixo:

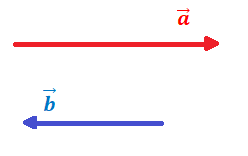
O módulo de um vetor é dado pelo seu valor numérico, sem esquecer-se da unidade de medida dessa grandeza, por exemplo, para velocidade devemos escrever: 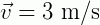$\vec{v}=3\text{ m/s}$. Já a direção de um vetor é diagonal, vertical ou horizontal. Por fim, o sentido de um vetor é direita, esquerda, cima ou baixo, leste ou oeste, etc., dependendo do sentido em que ele está agindo.

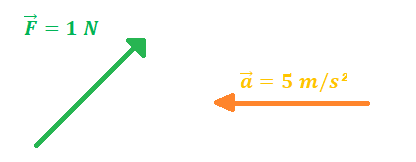
Nos exemplos acima, o vetor força ($\vec{F}$) tem módulo de 1 N, direção diagonal e sentido para cima, já o vetor aceleração ($\vec{a}$) tem módulo de 5 m/s², direção horizontal e sentido para esquerda.

Operações com vetores

As operações vetoriais não são realizadas da mesma forma que realizamos as operações com números. Vejamos as operações possíveis e como realizá-las:

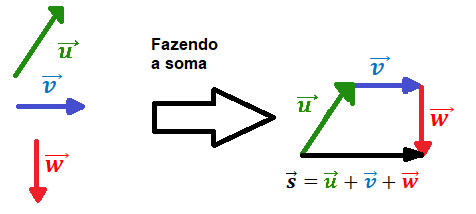
• Soma: para somarmos dois vetores, podemos utilizar a chamada Regra do Polígono, onde, basicamente, colocamos cada vetor enfileirado um com o outro. Por fim, escrevemos o vetor soma (que fecha o polígono), de maneira que o seu início coincida com o início do primeiro vetor e seu final coincida com o final do último vetor. Veja um exemplo abaixo, onde somamos os vetores $\vec{u}$, $\vec{v}$ e $\vec{w}$:

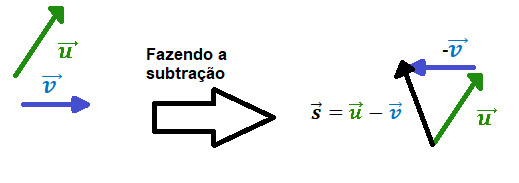
• Subtração: também utilizamos a regra do polígono, porém invertemos o sentido do vetor a ser subtraído. Veja o exemplo onde subtraímos os vetores $\vec{u}$ e $\vec{v}$:

• Decomposição de vetores: a ideia aqui é decompor um vetor sobre os eixos cartesianos, de forma que as operações que serão realizadas com ele sejam facilitadas. Vejamos como realizar isso a partir de um exemplo:

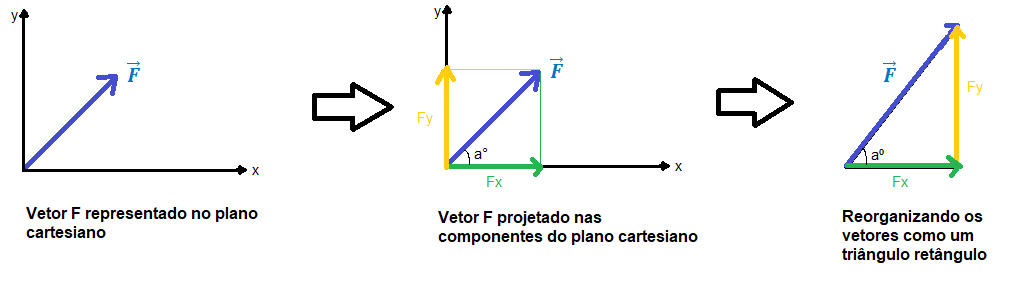
Escrevemos o vetor 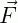$\vec{F}$ no plano cartesiano e em seguida projetamos suas componentes nos eixos x e y. Em seguida, para encontrar esses valores, vamos reorganizar esses vetores de forma que eles formem triângulo retângulo e, utilizando trigonometria, podemos escrever as componentes desses vetores como:

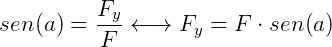
$sen(a)=\frac{F_y}{F}\longleftrightarrow F_y=F\cdot sen(a)$ 

e

$cos(a)=\frac{F_x}{F}\longleftrightarrow F_x=F\cdot cos(a)$ 

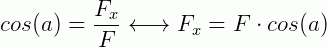
Ou, podemos escrever F como a soma vetorial:

$F=\sqrt{F^2_x+F^2_y}$

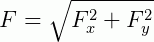
• Produto de um vetor por um número real: o produto entre o número k e o vetor $\vec{u}$ fornece um vetor $\vec{w}$, de mesma direção que o vetor $\vec{u}$, porém o sentido varia se k>0 (mesmo sentido que $\vec{u}$) ou k<0 (sentido oposto ao de $\vec{u}$).
• Produto dois vetores: Sejam os vetores $\vec{u}=(x_1 \hat{i}, y_1 \hat{j}, z_1 \hat{k})$ e $\vec{v}=(x_2 \hat{i}, y_2 \hat{j}, z_2 \hat{k})$, dados em função das suas coordenadas no plano cartesiano, temos que:
  • Produto escalar (ou produto interno): é a multiplicação entre dois vetores, resultando num escalar, e é obtida multiplicando componente a componente do vetor:

$\vec{u}\cdot\vec{v}=x_1\cdot x_2 + y_1\cdot y_2 + z_1\cdot z_2$

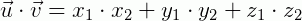
• • • Produto vetorial (ou produto externo): é a multiplicação entre dois vetores que resulta em outro vetor. É obtido de maneira mais complexa e pode utilizar o ângulo entre esses vetores:

$\vec{u}\times\vec{v}=\left( \begin{array}{ccc}\hat{i} &\hat{j}&\hat{k}\\x_1&y_1&z_1\\x_2&y_2&z_2\end{array}\right)\longleftrightarrow$

$\longleftrightarrow\vec{u}\times\vec{v}=(y_1\cdot z_2 -z_1\cdot y_2)\hat{i}-(x_1\cdot z_2-z_1\cdot x_2)\hat{j}+(x_1\cdot y_2-y_1\cdot x_2)\hat{k}$

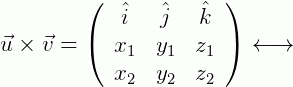
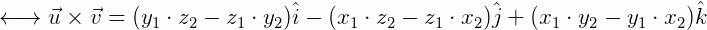
Referências:

MIRANDA, Daniel; GRISI, Rafael; LODOVICI, Sinuê. Geometria Analítica e Vetorial. Notas de aula do curso de Geometria Analítica da Universidade Federal do ABC (UFABC). Versão 13. Santo André, julho de 2020.

Texto originalmente publicado em https://www.infoescola.com/fisica/vetores/