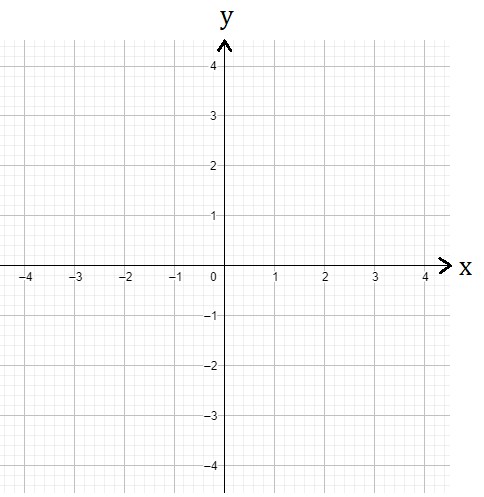
O plano cartesiano é um sistema de coordenadas que leva esse nome devido ao seu criador, o matemático e filósofo René Descartes. Vamos tratar aqui os aspectos do plano cartesiano em duas dimensões, ou seja, duas orientações: A horizontal, que chamamos de abcissa ou eixo x, e a vertical, que chamamos de ordenada ou eixo y, configurando assim duas dimensões no espaço. O plano cartesiano é uma ferramenta muito útil quando estudamos geometria analítica, na representação e/ou construção de gráficos de funções. Abaixo, uma ilustração do plano cartesiano:
É importante lembrar do conceito das relações binárias da teoria dos conjuntos pois, é a partir daí que podemos construir um plano cartesiano conveniente para o nosso estudo. Por exemplo, quando estudamos funções, onde o domínio e o contradomínio pertencem aos reais, tanto o eixo x quanto o y são retas que possuem todos os números reais. Neste exemplo, o plano no qual estudaríamos seria aquele formado pela relação binária 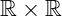 , ou simplesmente
, ou simplesmente 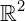 .
.
Conteúdo deste artigo
Localizando pontos no plano cartesiano
Antes de pensarmos no uso do plano para traçar gráficos, devemos antes entender como uma coordenada é representada. Ainda pensando em duas dimensões, cada ponto será descrito por uma coordenada do tipo (x, y) onde, o valor de x será o seu correspondente no eixo x e o valor de y, seu correspondente no eixo y. Veja a figura abaixo a representação dos pontos (2,1), (-3,2), (-2,-2) e (3,-3). Cada ponto está posicionado em um quadrante onde, a partir do primeiro, os outros 3 são dispostos no sentido anti-horário ao plano.
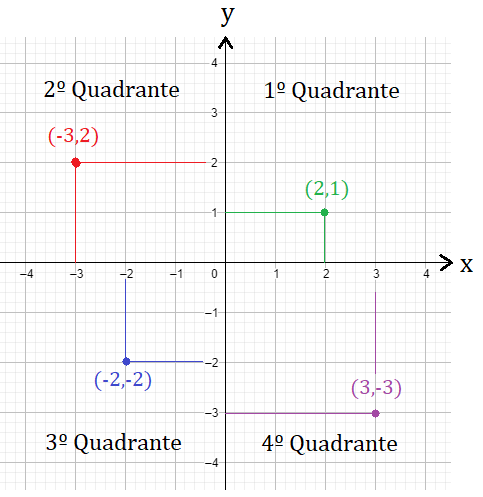
Note que como x e y são nada mais do que retas reais, o ponto central (0,0) representa tanto o 0 na reta do x quanto na reta do y. Sendo assim, para cima ou para direita do plano, os números serão sempre positivos (+). Para baixo ou para a esquerda, serão negativos (-).
Distância entre pontos
Dados dois pontos distintos, A(x1, y1) e B(x2, y2). Para determinarmos a distância entre dois pontos quaisquer no plano cartesiano podemos utilizar o teorema de Pitágoras. Veja:
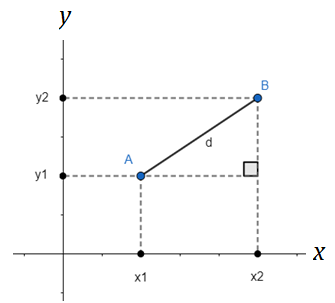
A distância d entre os pontos A e B, como mostra a figura, pode ser a hipotenusa de um triângulo retângulo, sendo seus catetos as distâncias entre os valores x1 e x2 e também, y1 e y2. Para sabermos a distância entre dois números na reta real, basta calcular a diferença entre ambos. Mesmo que essa diferença gere um resultado negativo não precisamos nos preocupar, pois quando lidamos com distâncias estamos sempre levando em consideração o módulo deste valor, ou seja, sempre será um valor positivo (note que a diferença entre os valores está ao quadrado). Então, só nos resta obter a fórmula da distância entre dois pontos. Utilizando o teorema de Pitágoras:
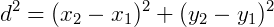
Então, temos:
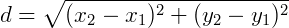
Espaço em 3 dimensões
O espaço em três dimensões tem algumas diferenças em relação ao de duas dimensões. Veja a figura abaixo:
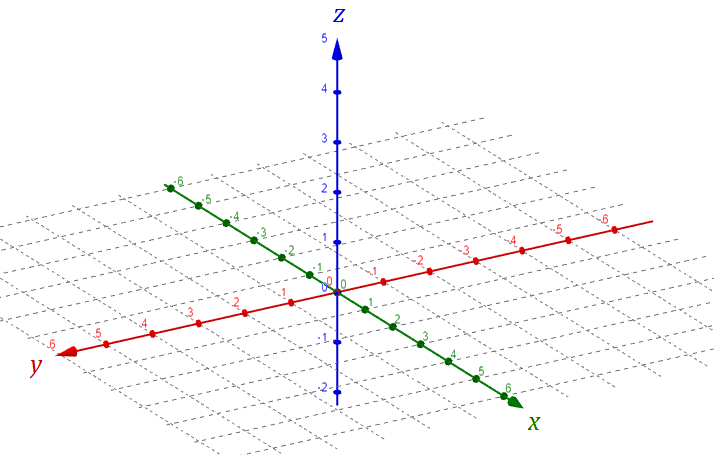
Agora, um novo eixo aparece, perpendicular ao plano cartesiano (x, y), o eixo z. Ele também é uma reta real e o seu marco zero é coincidente com o ponto (0,0) no plano (x, y) . Agora, para determinarmos um ponto neste espaço devemos acrescentar uma nova coordenada, o que nos leva a representação de qualquer ponto no espaço como (x, y, z).
A distância entre dois pontos no espaço continua seguindo a mesma regra do teorema de Pitágoras, porém com uma coordenada a mais:
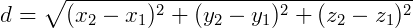
Referências Bibliográficas:
GUIDORIZZI, Hamilton L. Um Curso de Cálculo: Volume 1. Rio de Janeiro: Editora LTC, 2001.
WINTERLE, Paulo. Vetores e Geometria Analítica. São Paulo: Pearson Makron Books, 2000.
Texto originalmente publicado em https://www.infoescola.com/matematica/plano-cartesiano/