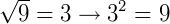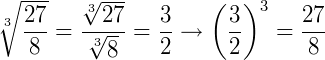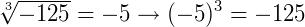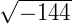Para iniciar os estudos sobre radiciação, vamos introduzir o conceito de radicais. Seja a igualdade 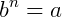 dizemos que b é a raiz enésima de a, ou seja:
dizemos que b é a raiz enésima de a, ou seja:
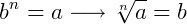
O símbolo 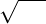 é conhecido por radical, a é o radicando e n é o índice. Em outro caso, se b=2, b é a raiz quadrada de a. Se b=3, b é a raiz cúbica de a. Abaixo, alguns exemplos:
é conhecido por radical, a é o radicando e n é o índice. Em outro caso, se b=2, b é a raiz quadrada de a. Se b=3, b é a raiz cúbica de a. Abaixo, alguns exemplos:



 não é um número real. Não existe um número real que quando elevado ao quadrado nos retorne um valor negativo.
não é um número real. Não existe um número real que quando elevado ao quadrado nos retorne um valor negativo.
Veja abaixo as condições de existência dos radicais:
Conteúdo deste artigo
Condição de existência de radicais
Raízes com índices pares de números negativos não existem nos reais:
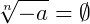 para n=2, 4, 6, ...
para n=2, 4, 6, ...
Já com índices impares é possível. No caso:
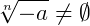 para n=3, 5, 7, ...
para n=3, 5, 7, ...
Propriedades da radiciação
1. 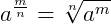
2. 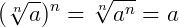
3. 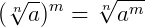
4. 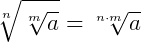
5. 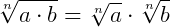
6. 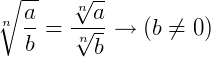
7. 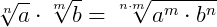
8. 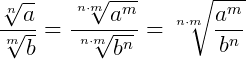
9. 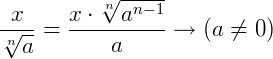
10. 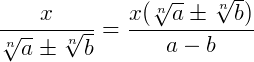
Repare na propriedade (9). Este processo consiste em retirar as raízes do denominador das frações, que é o que chamamos de racionalização. Quando um denominador está na forma 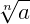 devemos multiplicar o numerador e o denominador por
devemos multiplicar o numerador e o denominador por 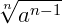 .
.
Calculando o valor de raízes
O método mais comum para calcular raízes de qualquer índice é aquele em que decompomos o radicando como um produto de fatores primos. Vamos por exemplo calcular a raiz quadrada de 16:
Se decompormos o 16 em um produto de fatores primos obtemos:
16 = 2 . 2 . 2 . 2 = 24
Logo podemos dizer que:
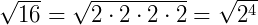
Pela propriedade número (3) podemos escrever como:
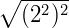
Como o índice de uma raiz quadrada é dois, então, pela propriedade (2), temos:
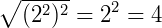
Então, 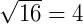 .
.
Mais um exemplo, mas agora para raiz quadrada de 12. Podemos dizer que:
12= 2 . 2 . 3 = 22 . 3
Reescrevendo, temos:
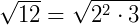
Note que se utilizarmos a propriedade número (5) podemos dizer que:
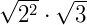
O que nos dá:
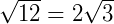
Como 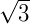 é um número irracional, então podemos apenas deixá-lo indicado na expressão.
é um número irracional, então podemos apenas deixá-lo indicado na expressão.
Leia também:
Referências Bibliográficas
DEMANDA, Franklin D; WAITS, Bert K.; FOLEY, Gregory D.; KENNEDY, Daniel. Pré Calculo. São Paulo: Pearson, 2013.
MORGADO, A. C.; WAGNER, E.; JORGE, M. Álgebra I. São Paulo: Livraria Francisco Alves Editora S.A., 1974.
Texto originalmente publicado em https://www.infoescola.com/matematica/radiciacao/