Regra de Chió

Ouça este artigo:

Um determinante é uma função matricial que associa uma matriz quadrada a um número real e, normalmente é utilizado para informar se uma matriz estudada tem ou não inversa. Sua forma como conhecemos, aparece em 1812, num trabalho de Cauchy, e surge como uma tentativa de resolver sistemas lineares. Daí sua importância até hoje, já que no dia a dia resolvemos problemas com sistemas lineares gigantescos, e poder reduzir esses sistemas a números facilita muito, além de economizar tempo e dinheiro.

Quando queremos calcular (manualmente) o determinante de matrizes grandes, uma ideia é realizar algum tipo de procedimento até reduzir a ordem dessa matriz. Existem várias regras ou métodos para fazer isso, um deles é a chamada Regra de Chió.

A ideia da Regra de Chió é reduzir a ordem de uma matriz A, de ordem n ≥ 2, para facilitar o cálculo do determinante. Interessante, mas será que essa regra pode ser utilizada em qualquer matriz? A resposta é: não! Para ser possível utilizar a regra de Chió é necessário que algum elemento da matriz seja igual a 1, ou seja, devemos ter um a_ij = 1 (lembrando que nessa notação, a_ij é um elemento da matriz A, com i linhas e j colunas).

A segunda questão que pode surgir é: se eu quero saber o determinante da matriz A o que me ajuda encontrar outra matriz? Bem, ao utilizarmos a Regra de Chió em uma matriz A de ordem n (com n ≥ 2), obtemos uma nova matriz B, de ordem (n-1), tal que: det(A) = (-1)^i+j . det(B), onde i e j são respectivamente a linha e a coluna do elemento a_ij = 1.

Para utilizarmos essa técnica devemos seguir os seguintes passos: 1) Localizar o elemento igual a 1 que vamos utilizar, 2) Isolarmos a linha e a coluna a que esse elemento pertence, 3) Subtrair de cada elemento restante o produto dos dois elementos isolados, pertencentes a linha e coluna que esse elemento pertence e obteremos uma nova matriz e 4) realizamos esse processo até obtermos uma matriz cuja ordem sejamos capazes de resolver o determinante.

Para entender melhor como a regra de Chió funciona, vamos ver um exemplo.

Seja a matriz 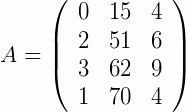$A=\left(\begin{array}{ccc}0&15&4\\2&51&6\\3&62&9\\1&70&4\end{array}\right)$ , vamos encontrar o determinante de A utilizando a regra de Chió (obs. De antemão avisamos que det(A) = -4).

Solução:

Localizar o elemento 1 que vamos usar. R: a₁₂=1.
Isolarmos a linha e a coluna a que esse elemento pertence.

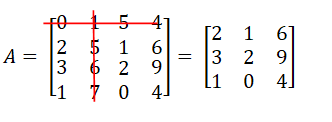
Subtrair de cada elemento restante o produto dos dois elementos isolados, pertencentes à linha e coluna que esse elemento pertence.

Olhando para o elemento a₂₁= 2, vemos que os elementos da linha e da coluna aos quais ele pertence são: a₁₁= 0 e o a₂₂= 5. Assim o elemento que vamos subtrair de a₂₁= 2 será 0.5=0.
O elemento a₄₄= 4. Para a linha e coluna a que ele pertence, foram removidos os elementos a₄₂= 7 e o a₁₄= 4. Então removeremos de a₄₄= 4 o elemento 7.4. Seguindo a mesma ideia temos para os outros elementos temos que:

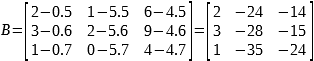
Para calcular o determinante da matriz B utilizamos (por exemplo, utilizando a Regra de Sarrus), encontramos que:

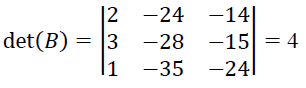
Assim, o determinante da matriz A será:

Ou seja, chegamos ao valor desejado de maneira bem mais simples.

Observações importantes:

Quando o elemento 1 estiver na primeira linha, a visualização dos valores a serem multiplicados é mais fácil, no entanto, podemos utilizar qualquer elemento 1 presente na nossa matriz.
E se a minha matriz não tiver o elemento 1 em nenhuma posição? Você poderia utilizar algum método para obter um determinante equivalente (por exemplo, o Teorema de Jacobi) que tenha um elemento 1.
Se quiséssemos poderíamos utilizar a regra de Chió novamente e reduzir a matriz B a uma matriz C, de ordem 2. Vamos fazer para verificar que ainda assim isso daria certo.

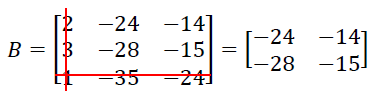
Escolhendo o elemento a₃₁=1, e realizando os mesmos procedimentos que realizamos para a matriz A temos que:

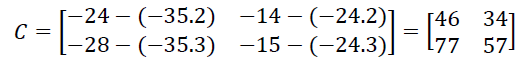
Disso, temos que: det(𝐶) = 4. Então:

Novamente chegamos ao resultado esperado, mostrando que a Regra de Chió é pode ser muito útil para cálculo de determinantes de ordem n ≥ 2.

Referências:

COSTA, Júlio César. Determinantes e Seus Teoremas uma Nova Proposta Para o Ensino Médio. Tese (Título de Especialista em Matemática) – Instituto de Ciências Exatas, Universidade Federal de Minas Gerais. Belo Horizonte, 2016.

REAMAT. Determinantes. Disponível em: <https://www.ufrgs.br/reamat/AlgebraLinear/livro/s9-determinantes.html>. Acessado em 18/11/2021. Universidade Federal do Rio Grande do Sul (UFRGS), 2020.

Texto originalmente publicado em https://www.infoescola.com/matematica/regra-de-chio/