Volume do cilindro

No texto de volume do prisma, temos, pelo Princípio de Cavaliere, que o volume de prismas e cilindros é dado pela multiplicação da área da base pela altura.

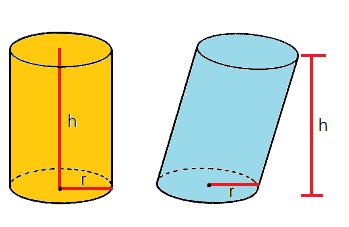Considerando um cilindro de raio r e altura h.

A área da base será 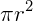$\pi r^2$.

Multiplicando a área da base pela altura, temos: 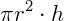$\pi r^2 \cdot h$.

Portanto, o volume do cilindro é:

$\pi r^2 \cdot h$

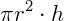
Exemplos:

1) Dado um cilindro de raio 3 cm e altura 7 cm. Qual é o seu volume?

Resposta:

• r = 3 cm.
• h = 7 cm.

$V = \pi r^2 \cdot h$

$V = \pi 9 \cdot 7$

$V = 63\pi cm^3$

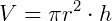
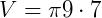
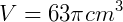
Observação: se considerarmos 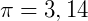$\pi = 3,14$, o volume é aproximadamente 197,82 cm³.

2) Um cilindro tem raio 2 cm e volume de 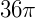$36\pi$ cm ³. Qual é sua altura?

Resposta:

• r = 2 cm.
• h = ?

$V = \pi r^2 \cdot h$

$36\pi = \pi 2^2 \cdot h$

$36 = 4h$

$h = \frac{36}{4} = 9 cm$

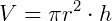
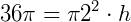
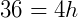
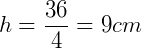
3) Um cilindro tem altura 16 cm e volume 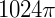$1024 \pi$ cm³. Qual é seu raio?

Resposta:

• r = ?
• h = 16 cm.

$V = \pi r^2 \cdot h$

$1024\pi = \pi r^2 \cdot 16$

$1024 = 16r^2$

$r^2 = \frac{1024}{16}$

$r = \sqrt{64} = 8 cm$

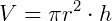
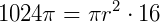
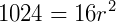
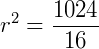
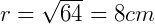
Observação: Quando a altura de um cilindro é o dobro do raio, chamamos o cilindro de equilátero.

Texto originalmente publicado em https://www.infoescola.com/matematica/volume-do-cilindro/